Câu hỏi: Trong mặt phẳng \(Oxy\) cho đường thẳng \(d\) có phương trình \(3x-y-9=0\). Tìm phép tịnh tiến theo vectơ có phương song song với trục \(Ox\) biến \(d\) thành đường thẳng \(d’\) đi qua gốc tọa độ và viết phương trình đường thẳng \(d’\).
Phương pháp giải
Tìm điểm đầu, điểm cuối của vectơ tịnh tiến lần lượt thuộc đường thẳng \(d\) và \(d’\).
Tính chất của phép tịnh tiến: Phép tịnh tiến biến một đường thẳng thành một đường thẳng song song với đường thẳng ban đầu để tìm phương trình đường thẳng \(d’\).
Lời giải chi tiết
Phép tịnh tiến theo vectơ có phương song song với trục \(Ox\), do đó \(Ox\) chứa vectơ tịnh tiến. Giao của \(d\) với trục \(Ox\) là điểm \(A(3; 0)\). Phép tịnh tiến phải tìm có vectơ tịnh tiến \(\vec v=\vec {AO}=(-3; 0)\).
Đường thẳng \(d’\) song song với \(d\) và đi qua gốc tọa độ nên nó có phương trình \(3x-y=0\).
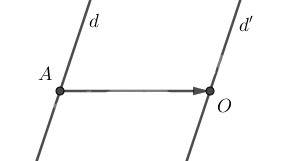
Tìm điểm đầu, điểm cuối của vectơ tịnh tiến lần lượt thuộc đường thẳng \(d\) và \(d’\).
Tính chất của phép tịnh tiến: Phép tịnh tiến biến một đường thẳng thành một đường thẳng song song với đường thẳng ban đầu để tìm phương trình đường thẳng \(d’\).
Lời giải chi tiết
Phép tịnh tiến theo vectơ có phương song song với trục \(Ox\), do đó \(Ox\) chứa vectơ tịnh tiến. Giao của \(d\) với trục \(Ox\) là điểm \(A(3; 0)\). Phép tịnh tiến phải tìm có vectơ tịnh tiến \(\vec v=\vec {AO}=(-3; 0)\).
Đường thẳng \(d’\) song song với \(d\) và đi qua gốc tọa độ nên nó có phương trình \(3x-y=0\).