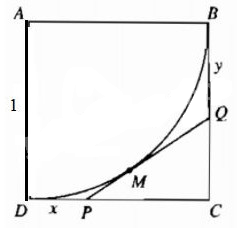
Câu hỏi: Cho hình vuông ABCD với cạnh có độ dài bằng 1 và cung BD là một phần tư đường tròn tâm A, bán kính AB chứa trong hình vuông (h. 1.4). Tiếp tuyến tại M của cung BD cắt đoạn thẳng CD tại điểm P và cắt đoạn thẳng BC tại điểm Q. Đặt x = DP và y = BQ
\(P{Q^2} = {x^2} + {y^2} - 2x - 2y + 2\) và \(PQ = x + y\)
Từ đó tính y theo x
Lời giải chi tiết:
Tam giác PCQ vuông tại C có \(PC = 1 - x, QC = 1 - y\) và vuông tại C nên theo Pitago ta có:
\(\begin{array}{l}P{Q^2} = P{C^2} + C{Q^2}\\ = {\left( {1 - x} \right)^2} + {\left({1 - y} \right)^2}\\ = 1 - 2x + {x^2} + 1 - 2y + {y^2}\\ = {x^2} + {y^2} - 2x - 2y + 2\end{array}\)
Lại có,
BC, QP là tiếp tuyến với đường tròn \(\left( {A; AB} \right)\) cắt nhau tại Q nên \(QM = QB = y\)
DC, QP là tiếp tuyến với đường tròn \(\left( {A; AB} \right)\) cắt nhau tại P nên \(PM = PD = y\)
Vậy \(PQ = PM + MQ = x + y\).
\(\begin{array}{l}
\Rightarrow P{Q^2} = {\left({x + y} \right)^2} = {x^2} + 2xy + {y^2}\\
\Rightarrow {x^2} + {y^2} - 2x - 2y + 2 = {x^2} + 2xy + {y^2}\\
\Leftrightarrow 2xy + 2x + 2y - 2 = 0\\
\Leftrightarrow xy + x + y - 1 = 0\\
\Leftrightarrow y\left({x + 1} \right) = 1 - x\\
\Leftrightarrow y = \frac{{1 - x}}{{x + 1}}
\end{array}\)
Vậy \(y = {{1 - x} \over {x + 1}}, 0 < x < 1\)
Lời giải chi tiết:
\(\begin{array}{l}
PQ = x + y = x + \frac{{1 - x}}{{x + 1}}\\
= \frac{{{x^2} + x + 1 - x}}{{x + 1}} = \frac{{{x^2} + 1}}{{x + 1}}
\end{array}\)
Do đó, \(PQ = {{{x^2} + 1} \over {x + 1}}, 0 < x < 1\).
Xét hàm
\(\begin{array}{l}
f\left(x \right) = \frac{{{x^2} + 1}}{{x + 1}}\\
f'\left(x \right) = \frac{{2x\left({x + 1} \right) - \left({{x^2} + 1} \right)}}{{{{\left({x + 1} \right)}^2}}}\\
= \frac{{{x^2} + 2x - 1}}{{{{\left({x + 1} \right)}^2}}}\\
f'\left(x \right) = 0 \Leftrightarrow {x^2} + 2x - 1 = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = \sqrt 2 + 1 \notin \left({0; 1} \right)\\
x = \sqrt 2 - 1 \in \left({0; 1} \right)
\end{array} \right.
\end{array}\)
Do đó, đoạn thẳng PQ có độ dài nhỏ nhất khi \(x = \sqrt 2 - 1\)

Câu a
Chứng minh rằng\(P{Q^2} = {x^2} + {y^2} - 2x - 2y + 2\) và \(PQ = x + y\)
Từ đó tính y theo x
Lời giải chi tiết:
Tam giác PCQ vuông tại C có \(PC = 1 - x, QC = 1 - y\) và vuông tại C nên theo Pitago ta có:
\(\begin{array}{l}P{Q^2} = P{C^2} + C{Q^2}\\ = {\left( {1 - x} \right)^2} + {\left({1 - y} \right)^2}\\ = 1 - 2x + {x^2} + 1 - 2y + {y^2}\\ = {x^2} + {y^2} - 2x - 2y + 2\end{array}\)
Lại có,
BC, QP là tiếp tuyến với đường tròn \(\left( {A; AB} \right)\) cắt nhau tại Q nên \(QM = QB = y\)
DC, QP là tiếp tuyến với đường tròn \(\left( {A; AB} \right)\) cắt nhau tại P nên \(PM = PD = y\)
Vậy \(PQ = PM + MQ = x + y\).
\(\begin{array}{l}
\Rightarrow P{Q^2} = {\left({x + y} \right)^2} = {x^2} + 2xy + {y^2}\\
\Rightarrow {x^2} + {y^2} - 2x - 2y + 2 = {x^2} + 2xy + {y^2}\\
\Leftrightarrow 2xy + 2x + 2y - 2 = 0\\
\Leftrightarrow xy + x + y - 1 = 0\\
\Leftrightarrow y\left({x + 1} \right) = 1 - x\\
\Leftrightarrow y = \frac{{1 - x}}{{x + 1}}
\end{array}\)
Vậy \(y = {{1 - x} \over {x + 1}}, 0 < x < 1\)
Câu b
Tính PQ theo x và tìm x để PQ có độ dài nhỏ nhất.Lời giải chi tiết:
\(\begin{array}{l}
PQ = x + y = x + \frac{{1 - x}}{{x + 1}}\\
= \frac{{{x^2} + x + 1 - x}}{{x + 1}} = \frac{{{x^2} + 1}}{{x + 1}}
\end{array}\)
Do đó, \(PQ = {{{x^2} + 1} \over {x + 1}}, 0 < x < 1\).
Xét hàm
\(\begin{array}{l}
f\left(x \right) = \frac{{{x^2} + 1}}{{x + 1}}\\
f'\left(x \right) = \frac{{2x\left({x + 1} \right) - \left({{x^2} + 1} \right)}}{{{{\left({x + 1} \right)}^2}}}\\
= \frac{{{x^2} + 2x - 1}}{{{{\left({x + 1} \right)}^2}}}\\
f'\left(x \right) = 0 \Leftrightarrow {x^2} + 2x - 1 = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = \sqrt 2 + 1 \notin \left({0; 1} \right)\\
x = \sqrt 2 - 1 \in \left({0; 1} \right)
\end{array} \right.
\end{array}\)
Do đó, đoạn thẳng PQ có độ dài nhỏ nhất khi \(x = \sqrt 2 - 1\)
Rất tiếc, câu hỏi này chưa có lời giải chi tiết. Bạn ơi, đăng nhập và giải chi tiết giúp zix.vn nhé!!!