Trong không gian với hệ trục tọa độ $O x y z$ cho ba mặt phẳng...

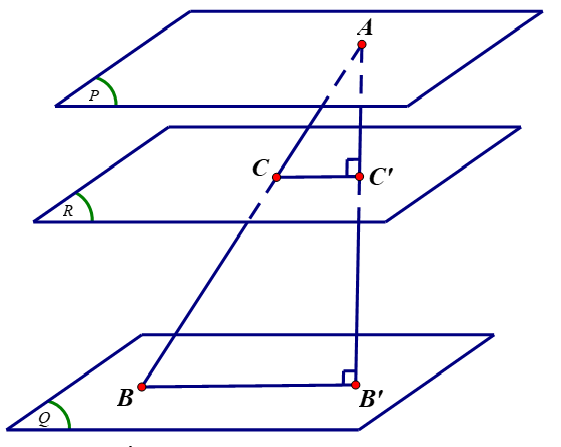
Ta có $M(1 ; 0 ; 0) \in(P)$ và ba mặt phẳng $(P),(Q),(R)$ đôi một song song với nhau. Gọi $B^{\prime}, C^{\prime}$ lần lượt là hình chiếu vuông góc của $A$ trên các mặt phẳng $(Q),(R)$, ta có:
$
\begin{aligned}
& A B^{\prime}=d(A ;(Q))=d(M ;(Q))=\dfrac{|1-2.0+0+8|}{\sqrt{1^2+(-2)^2+1^2}}=\dfrac{3 \sqrt{6}}{2} . \\
& A C^{\prime}=d(A ;(R))=d(M ;(R))=\dfrac{|1-2.0+0-4|}{\sqrt{1^2+(-2)^2+1^2}}=\dfrac{\sqrt{6}}{2} .
\end{aligned}
$
Do $A B^{\prime}=3 A C^{\prime}$ nên đặt $C C^{\prime}=a \Rightarrow B B^{\prime}=3 a$.
Ta có $A B^2=A B^{\prime 2}+B B^{\prime 2}=\dfrac{27}{2}+9 a^2 ; A C=\sqrt{A C^{\prime 2}+C C^{\prime 2}}=\sqrt{\dfrac{3}{2}+a^2}$.
Nên: $T=A B^2+\dfrac{144}{A C}=\dfrac{27}{2}+9 a^2+\dfrac{144}{\sqrt{\dfrac{3}{2}+a^2}}=9\left(\dfrac{3}{2}+a^2\right)+\dfrac{72}{\sqrt{\dfrac{3}{2}+a^2}}+\dfrac{72}{\sqrt{\dfrac{3}{2}+a^2}}$
$
\geq 3 \sqrt[3]{9\left(\dfrac{3}{2}+a^2\right) \cdot \dfrac{72}{\sqrt{\dfrac{3}{2}+a^2}} \cdot \dfrac{72}{\sqrt{\dfrac{3}{2}+a^2}}}=108 \text {. }
$
Do đó $\min T=108$ khi $a=\dfrac{\sqrt{2}}{2}$.