Google
Câu hỏi: Trong không gian $Oxyz$, xét mặt cầu $\left( S \right)$ có tâm $I\left( 3;7;12 \right)$ và bán kính $R$ thay đổi. Có bao nhiêu giá trị nguyên của $R$ sao cho ứng với mỗi giá trị đó, tồn tại hai tiếp tuyến của $\left( S \right)$ trong mặt phẳng $\left( Oyz \right)$ mà hai tiếp tuyến đó cùng đi qua $O$ và góc giữa chúng không nhỏ hơn $60{}^\circ $ ?
A. $11$.
B. $7$.
C. $5$.
D. $3$.
A. $11$.
B. $7$.
C. $5$.
D. $3$.
Để tồn tại tiếp tuyến thì mặt cầu $\left( S \right)$ phải cắt hoặc tiếp xúc mặt phẳng $\left( Oyz \right)$ nên $R\ge 3$.
Gọi $J$ là hình chiếu của $I$ lên mặt phẳng $\left( Oyz \right)$ ta có $J\left( 0;7;12 \right)$ và $IJ=3$ và $OJ=\sqrt{193}$.
Xét 2 tiếp tuyến đi qua $O$ và tiếp xúc với $\left( C \right)$ tại $K,H$ như hình vẽ.
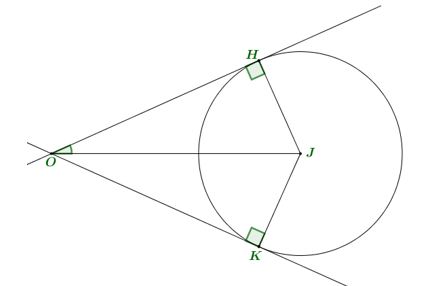Từ đề bài ta có $OJ.\sin 60{}^\circ >r\ge OJ.\sin 30{}^\circ \Leftrightarrow \dfrac{\sqrt{193}}{2}\le r<\sqrt{193}.\dfrac{\sqrt{3}}{2}$, với $r=JK=JH$.
Mà $d\left( I , \left( Oyz \right) \right)=IJ=3$ nên:
$\dfrac{193}{4}+{{d}^{2}}\left( I , \left( Oyz \right) \right)\le {{r}^{2}}+{{d}^{2}}\left( I , \left( Oyz \right) \right)<\dfrac{579}{4}+{{d}^{2}}\left( I , \left( Oyz \right) \right)$
$\Leftrightarrow \dfrac{193}{4}+9\le {{R}^{2}}<\dfrac{579}{4}+9\Leftrightarrow \dfrac{229}{4}\le {{R}^{2}}<\dfrac{615}{4}$
$\Leftrightarrow 7,6\approx \sqrt{\dfrac{229}{4}}\le R<\sqrt{\dfrac{615}{4}}\approx 12,4$, do $R\in \mathbb{Z}\Rightarrow R\in \left\{ 8;9;10;11;12 \right\}$.
Vậy, có 5 giá trị nguyên thỏa yêu cầu.
Gọi $J$ là hình chiếu của $I$ lên mặt phẳng $\left( Oyz \right)$ ta có $J\left( 0;7;12 \right)$ và $IJ=3$ và $OJ=\sqrt{193}$.
Xét 2 tiếp tuyến đi qua $O$ và tiếp xúc với $\left( C \right)$ tại $K,H$ như hình vẽ.
Mà $d\left( I , \left( Oyz \right) \right)=IJ=3$ nên:
$\dfrac{193}{4}+{{d}^{2}}\left( I , \left( Oyz \right) \right)\le {{r}^{2}}+{{d}^{2}}\left( I , \left( Oyz \right) \right)<\dfrac{579}{4}+{{d}^{2}}\left( I , \left( Oyz \right) \right)$
$\Leftrightarrow \dfrac{193}{4}+9\le {{R}^{2}}<\dfrac{579}{4}+9\Leftrightarrow \dfrac{229}{4}\le {{R}^{2}}<\dfrac{615}{4}$
$\Leftrightarrow 7,6\approx \sqrt{\dfrac{229}{4}}\le R<\sqrt{\dfrac{615}{4}}\approx 12,4$, do $R\in \mathbb{Z}\Rightarrow R\in \left\{ 8;9;10;11;12 \right\}$.
Vậy, có 5 giá trị nguyên thỏa yêu cầu.
Đáp án C.