Google
Câu hỏi: Trong không gian $Oxyz,$ cho mặt phẳng $\left( P \right):x-y+z+7=0,$ đường thẳng $d:\dfrac{x}{1}=\dfrac{y}{-2}=\dfrac{z}{2}$ và mặt cầu $\left( S \right):{{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z-2 \right)}^{2}}=5.$ Gọi $A, B$ là hai điểm trên mặt cầu $\left( S \right)$ và $AB=4;$ ${A}', {B}'$ là hai điểm nằm trên mặt phẳng $\left( P \right)$ sao cho $A{A}', B{B}'$ cùng song song với đường thẳng $d.$ Giá trị lớn nhất của tổng $A{A}'+ B{B}'$ gần nhất với giá trị nào sau đây
A. $13.$
B. $11.$
C. $12.$
D. $14.$
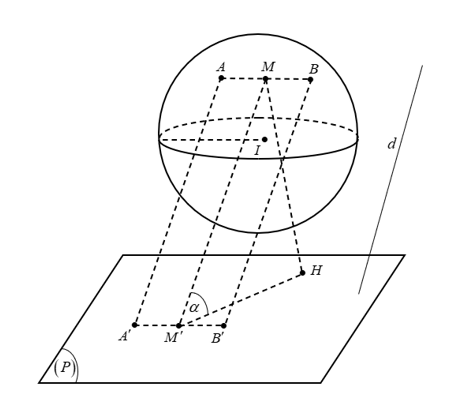Mặt cầu $\left( S \right)$ có tâm $I\left( 1;0;2 \right)$ và bán kính $R=\sqrt{5}$.
Khi đó khoảng cách: $d\left( I;\left( P \right) \right)=\dfrac{10\sqrt{3}}{3}>R$ nên $(P)$ và mặt cầu $(S)$ không giao nhau.
Gọi $M$ là trung điểm của $AB$, ${M}'$ là trung điểm của $A\prime B\prime $ thì:
$AA\prime +BB\prime =2M{M}'=2.\dfrac{MH}{\sin \left( M;\left( P \right) \right)}$.
Khi đó $M{{H}_{\max }}=\sqrt{{{R}^{2}}-\dfrac{A{{B}^{2}}}{4}}+d\left( I;\left( P \right) \right)=\sqrt{5-4}+\dfrac{10\sqrt{3}}{3}=\dfrac{3+10\sqrt{3}}{3}$.
Ta có $\sin \left( M;\left( P \right) \right)=\sin \left( d;\left( P \right) \right)=\dfrac{5\sqrt{3}}{9}$.
Vậy ${{\left( A{A}'+ B{B}' \right)}_{\max }}=2.\dfrac{\dfrac{3+10\sqrt{3}}{3}}{\dfrac{5\sqrt{3}}{9}}=\dfrac{60+6\sqrt{3}}{5}\approx 14,08$.
A. $13.$
B. $11.$
C. $12.$
D. $14.$
Khi đó khoảng cách: $d\left( I;\left( P \right) \right)=\dfrac{10\sqrt{3}}{3}>R$ nên $(P)$ và mặt cầu $(S)$ không giao nhau.
Gọi $M$ là trung điểm của $AB$, ${M}'$ là trung điểm của $A\prime B\prime $ thì:
$AA\prime +BB\prime =2M{M}'=2.\dfrac{MH}{\sin \left( M;\left( P \right) \right)}$.
Khi đó $M{{H}_{\max }}=\sqrt{{{R}^{2}}-\dfrac{A{{B}^{2}}}{4}}+d\left( I;\left( P \right) \right)=\sqrt{5-4}+\dfrac{10\sqrt{3}}{3}=\dfrac{3+10\sqrt{3}}{3}$.
Ta có $\sin \left( M;\left( P \right) \right)=\sin \left( d;\left( P \right) \right)=\dfrac{5\sqrt{3}}{9}$.
Vậy ${{\left( A{A}'+ B{B}' \right)}_{\max }}=2.\dfrac{\dfrac{3+10\sqrt{3}}{3}}{\dfrac{5\sqrt{3}}{9}}=\dfrac{60+6\sqrt{3}}{5}\approx 14,08$.
Đáp án D.
