Google
Câu hỏi: Trong không gian $Oxyz$, cho mặt cầu $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x-4y+6z-13=0$. Lấy điểm $M$ trong không gian sao cho từ $M$ kẻ được ba tiếp tuyến $MA$, $MB$, $MC$ đến mặt cầu $\left( S \right)$ thỏa mãn $\widehat{AMB}=60{}^\circ $, $\widehat{BMC}=90{}^\circ $, $\widehat{CMA}=120{}^\circ $ ( $A$, $B$, $C$ là các tiếp điểm). Khi đó đoạn thẳng $OM$ có độ nhỏ nhất bằng
A. $\sqrt{14}-3\sqrt{3}$.
B. $-\sqrt{14}+6\sqrt{3}$.
C. $\sqrt{14}-6$.
D. $6-\sqrt{14}$.
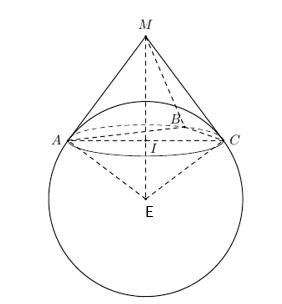Vì $MA$, $MB$, $MC$ là $3$ tiếp tuyến nên ta đặt $MA=MB=MC=x$.
$\vartriangle MAB$ có $MA=MB$, $\widehat{AMB}=60{}^\circ $ nên $\Delta MAB$ là tam giác đều, suy ra $AB=MA=MB=x$.
Áp dụng định lí Py-ta-go cho $\vartriangle MBC$ ta có $BC=\sqrt{M{{B}^{2}}+M{{C}^{2}}}=\sqrt{2{{x}^{2}}}=x\sqrt{2}.$
Áp dụng định lí hàm số cos cho $\vartriangle MCA$ : $CA=\sqrt{M{{A}^{2}}+M{{C}^{2}}-2MA.MC.\cos 120{}^\circ }=x\sqrt{3}$.
Nhận thấy $A{{B}^{2}}+B{{C}^{2}}={{x}^{2}}+2{{x}^{2}}=3{{x}^{2}}=A{{C}^{2}}$, suy ra $\vartriangle ABC$ vuông tại $B$.
Gọi $I$ là tâm đường tròn ngoại tiếp $\vartriangle ABC\Rightarrow I$ là trung điểm của $AC$.
Vì $MA=MB=MC$ nên $MI$ là trục đường tròn ngoại tiếp của $\vartriangle ABC$.
Do đó M; I; E thẳng hàng.
Mặt cầu $\left( S \right)$ có tâm $E\left( 1;2;-3 \right)$ bán kính $R=3\sqrt{3}=EC$
Suy ra $ME=\dfrac{EC}{\sin {{60}^{0}}}=6$. Vậy M thuộc mặt cầu $\left( S' \right)$ có tâm $E\left( 1;2;-3 \right)$ bán kính $R'=6$.
Ta có $OE=\sqrt{14}$
Vậy $Min OM=\left| OE-R' \right|=6-\sqrt{14}$.
A. $\sqrt{14}-3\sqrt{3}$.
B. $-\sqrt{14}+6\sqrt{3}$.
C. $\sqrt{14}-6$.
D. $6-\sqrt{14}$.
$\vartriangle MAB$ có $MA=MB$, $\widehat{AMB}=60{}^\circ $ nên $\Delta MAB$ là tam giác đều, suy ra $AB=MA=MB=x$.
Áp dụng định lí Py-ta-go cho $\vartriangle MBC$ ta có $BC=\sqrt{M{{B}^{2}}+M{{C}^{2}}}=\sqrt{2{{x}^{2}}}=x\sqrt{2}.$
Áp dụng định lí hàm số cos cho $\vartriangle MCA$ : $CA=\sqrt{M{{A}^{2}}+M{{C}^{2}}-2MA.MC.\cos 120{}^\circ }=x\sqrt{3}$.
Nhận thấy $A{{B}^{2}}+B{{C}^{2}}={{x}^{2}}+2{{x}^{2}}=3{{x}^{2}}=A{{C}^{2}}$, suy ra $\vartriangle ABC$ vuông tại $B$.
Gọi $I$ là tâm đường tròn ngoại tiếp $\vartriangle ABC\Rightarrow I$ là trung điểm của $AC$.
Vì $MA=MB=MC$ nên $MI$ là trục đường tròn ngoại tiếp của $\vartriangle ABC$.
Do đó M; I; E thẳng hàng.
Mặt cầu $\left( S \right)$ có tâm $E\left( 1;2;-3 \right)$ bán kính $R=3\sqrt{3}=EC$
Suy ra $ME=\dfrac{EC}{\sin {{60}^{0}}}=6$. Vậy M thuộc mặt cầu $\left( S' \right)$ có tâm $E\left( 1;2;-3 \right)$ bán kính $R'=6$.
Ta có $OE=\sqrt{14}$
Vậy $Min OM=\left| OE-R' \right|=6-\sqrt{14}$.
Đáp án D.