Google
Câu hỏi: Trong không gian $Oxyz$, cho hai điểm $A\left( 3;1;2 \right),B\left( -1;3;-2 \right)$ và đường thẳng $d:\dfrac{x-4}{2}=\dfrac{y-5}{-1}=\dfrac{z-3}{2}$. Mặt cầu $\left( S \right)$ qua hai điểm $A,B$ và tiếp xúc với đường thẳng $d$ có bán kính nhỏ nhất thì hoành độ tâm mặt cầu khi đó bằng
A. $3$.
B. $\dfrac{1}{4}$.
C. $\dfrac{5}{4}$.
D. $\dfrac{3}{2}$.
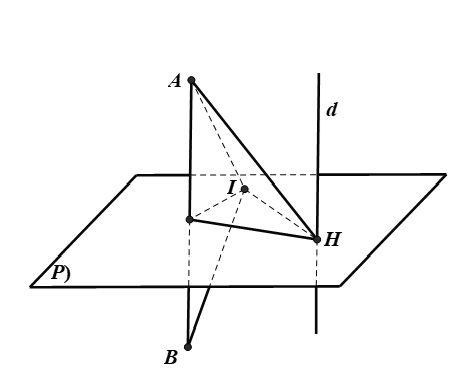Gọi mặt cầu $\left( S \right)$ có tâm $I$ và bán kính là $R$.
Mặt cầu $\left( S \right)$ qua hai điểm $A,B$ nên $I$ thuộc mặt phẳng $\left( P \right)$ là mặt phẳng trung trực của $AB$
Ta có $\left( P \right):2x-y+2z=0$.
Nhận xét thấy đường thẳng $d\bot \left( P \right)$ tại $H\left( 2;6;1 \right)$, hình chiếu vuông góc của $I$ lên $\left( d \right)$ là $H$. Do đó mặt cầu $\left( S \right)$ tiếp xúc với $\left( d \right)$ tại $H$.
Mặt cầu $\left( S \right)$ qua hai điểm $A,H$ nên $I$ thuộc mặt phẳng $\left( Q \right)$ là mặt phẳng trung trực của $AH$
Ta có $\left( Q \right):-2x+10y-2z-27=0$.
Vì $I\in \left( P \right);I\in \left( Q \right)$ nên $I\in \left( \Delta \right)$ với $\Delta $ là giao tuyến của $\left( P \right),\left( Q \right)$.
Ta có $\Delta :\left\{ \begin{aligned}
& x=1+t \\
& y=3 \\
& z=\dfrac{1}{2}-t \\
\end{aligned} \right.$$\Rightarrow I\left( 1+t;3;\dfrac{1}{2}-t \right)\Rightarrow R=AI=\sqrt{{{\left( t-2 \right)}^{2}}+4+{{\left( -t-\dfrac{3}{2} \right)}^{2}}}$
Hay $R=\sqrt{2{{t}^{2}}-t+\dfrac{41}{4}}$. Suy ra, ${{R}_{\min }}$ khi $t=\dfrac{1}{4}\Rightarrow I\left( \dfrac{5}{4};3;\dfrac{1}{4} \right)$
A. $3$.
B. $\dfrac{1}{4}$.
C. $\dfrac{5}{4}$.
D. $\dfrac{3}{2}$.
Mặt cầu $\left( S \right)$ qua hai điểm $A,B$ nên $I$ thuộc mặt phẳng $\left( P \right)$ là mặt phẳng trung trực của $AB$
Ta có $\left( P \right):2x-y+2z=0$.
Nhận xét thấy đường thẳng $d\bot \left( P \right)$ tại $H\left( 2;6;1 \right)$, hình chiếu vuông góc của $I$ lên $\left( d \right)$ là $H$. Do đó mặt cầu $\left( S \right)$ tiếp xúc với $\left( d \right)$ tại $H$.
Mặt cầu $\left( S \right)$ qua hai điểm $A,H$ nên $I$ thuộc mặt phẳng $\left( Q \right)$ là mặt phẳng trung trực của $AH$
Ta có $\left( Q \right):-2x+10y-2z-27=0$.
Vì $I\in \left( P \right);I\in \left( Q \right)$ nên $I\in \left( \Delta \right)$ với $\Delta $ là giao tuyến của $\left( P \right),\left( Q \right)$.
Ta có $\Delta :\left\{ \begin{aligned}
& x=1+t \\
& y=3 \\
& z=\dfrac{1}{2}-t \\
\end{aligned} \right.$$\Rightarrow I\left( 1+t;3;\dfrac{1}{2}-t \right)\Rightarrow R=AI=\sqrt{{{\left( t-2 \right)}^{2}}+4+{{\left( -t-\dfrac{3}{2} \right)}^{2}}}$
Hay $R=\sqrt{2{{t}^{2}}-t+\dfrac{41}{4}}$. Suy ra, ${{R}_{\min }}$ khi $t=\dfrac{1}{4}\Rightarrow I\left( \dfrac{5}{4};3;\dfrac{1}{4} \right)$
Đáp án C.
