Google
Câu hỏi: Trong không gian $Oxyz$, cho ba đường thẳng ${{d}_{1}}:\dfrac{x-1}{2}=\dfrac{y-1}{1}=\dfrac{z-1}{-2},$ ${{d}_{2}}:\dfrac{x-3}{1}=\dfrac{y+1}{2}=\dfrac{z-2}{2},$ ${{d}_{3}}:\dfrac{x-4}{2}=\dfrac{y-4}{-2}=\dfrac{z-1}{1}$. Mặt cầu bán kính nhỏ nhất tâm $I\left( a; b; c \right)$, tiếp xúc với 3 đường thẳng ${{d}_{1}}, {{d}_{2}}, {{d}_{3}}$. Giá trị tổng $S=a+2b+3c$ là
A. $11$.
B. $13$.
C. $10$.
D. $12$.
A. $11$.
B. $13$.
C. $10$.
D. $12$.
${{d}_{1}}$ đi qua điểm $A\left( 1;1;1 \right)$ có $VTCP \overrightarrow{ {{u}_{1}}}=\left( 2;1;-2 \right)$.
${{d}_{2}}$ đi qua điểm $B\left( 3;-1;2 \right)$ có $VTCP \overrightarrow{ {{u}_{2}}}=\left( 1;2;2 \right)$.
${{d}_{3}}$ đi qua điểm $C\left( 4;4;1 \right)$ có $VTCP \overrightarrow{{{u}_{3}}}=(2;-2;1)$.
Ta có: $\overrightarrow{{{u}_{1}}}.\overrightarrow{{{u}_{2}}}=0, \overrightarrow{{{u}_{2}}}.\overrightarrow{{{u}_{3}}}=0, \overrightarrow{{{u}_{3}}}.\overrightarrow{{{u}_{1}}}=0\Rightarrow \left( {{d}_{1}} \right),\left( {{d}_{2}} \right),\left( {{d}_{3}} \right)$ đôi một vuông góc với nhau.
$\left[ \overrightarrow{{{u}_{1}}}; \overrightarrow{{{u}_{2}}} \right].\overrightarrow{AB}\ne 0,\left[ \overrightarrow{{{u}_{2}}}; \overrightarrow{{{u}_{3}}} \right].\overrightarrow{BC}\ne 0,\left[ \overrightarrow{{{u}_{3}}},\overrightarrow{{{u}_{1}}} \right].\overrightarrow{CA}\ne 0\Rightarrow \left( {{d}_{1}} \right),\left( {{d}_{2}} \right),\left( {{d}_{3}} \right)$ đôi một chéo nhau.
Lại có: $\overrightarrow{AB}=\left( 2;-2;1 \right);\overrightarrow{AB}.\overrightarrow{ {{u}_{1}}}=0$ và $\overrightarrow{AB}. \overrightarrow{{{u}_{2}}}=0$ nên ${\left(d_{1}\right),\left(d_{2}\right),\left(d_{3}\right)}$ chứa 3 cạnh của hình hộp chữ nhật như hình vẽ.
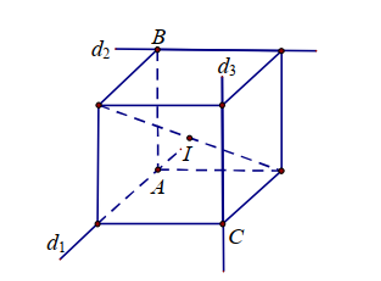Vì mặt cầu tâm ${I(a ; b ; c)}$ tiếp xúc với 3 đường thẳng ${\left(d_{1}\right),\left(d_{2}\right),\left(d_{3}\right)}$ nên bán kính
${R=d\left(I, d_{1}\right)=d\left(I, d_{2}\right)=d\left(I, d_{3}\right) \Leftrightarrow R^{2}=d^{2}\left(I, d_{1}\right)=d^{2}\left(I, d_{2}\right)=d^{2}\left(I, d_{3}\right)}$ $\Leftrightarrow {{R}^{2}}={{\left( \dfrac{\left| \left[ \overrightarrow{AI},{{{\vec{u}}}_{1}} \right] \right|}{\left| \overrightarrow{{{u}_{1}}} \right|} \right)}^{2}}={{\left( \dfrac{\left| \left[ \overrightarrow{BI},\overrightarrow{{{u}_{2}}} \right] \right|}{\left| \overrightarrow{{{u}_{2}}} \right|} \right)}^{2}}={{\left( \dfrac{\left| \left[ \overrightarrow{CI},\overrightarrow{{{u}_{3}}} \right] \right|}{\left| \overline{{{u}_{3}}} \right|} \right)}^{2}}$, ta thấy ${{\left| \overrightarrow{{{u}_{1}}} \right|}^{2}}={{\left| \overrightarrow{{{u}_{2}}} \right|}^{2}}={{\left| \overrightarrow{{{u}_{3}}} \right|}^{2}}=9$ và
$\overrightarrow{AI}=\left( a-1;b-1;c-1 \right),\left[ \overrightarrow{AI},\overrightarrow{{{u}_{1}}} \right]=\left( -2b-c+3;2a+2c-4;a-2b+1 \right)$.
$\overrightarrow{BI}=\left( a-3;b+1;c-2 \right), \left[ \overrightarrow{BI},\overrightarrow{{{u}_{2}}} \right]=\left( 2b-2c+6;-2a+c+4;2a-b-7 \right).$ ${}$
$\overrightarrow{CI}=\left( a-4;b-4;c-1 \right),\left[ \overrightarrow{CI},\overrightarrow{{{u}_{3}}} \right]=\left( b+2c-6;-a+2c+2;-2a-2b+16 \right).$
$9{{R}^{2}}={{\left| \left[ \overrightarrow{AI},{{{\vec{u}}}_{1}} \right] \right|}^{2}}={{\left| \left[ \overrightarrow{BI},\overrightarrow{{{u}_{2}}} \right] \right|}^{2}}={{\left| \left[ \overrightarrow{CI},\overrightarrow{{{u}_{3}}} \right] \right|}^{2}}\Rightarrow 27{{R}^{2}}={{\left| \left[ \overrightarrow{AI},{{{\vec{u}}}_{1}} \right] \right|}^{2}}+{{\left| \left[ \overrightarrow{BI},\overrightarrow{{{u}_{2}}} \right] \right|}^{2}}+{{\left| \left[ \overrightarrow{CI},\overrightarrow{{{u}_{3}}} \right] \right|}^{2}}$
$=18\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)-126a-54b-54c+423=18{{\left( a-\dfrac{7}{2} \right)}^{2}}+18{{\left( b-\dfrac{3}{2} \right)}^{2}}+18{{\left( c-\dfrac{3}{2} \right)}^{2}}+\dfrac{243}{2}\ge \dfrac{243}{2}$ $\Rightarrow {{R}_{\min }}=\dfrac{3\sqrt{2}}{2}\approx 2,12$ khi $a=\dfrac{7}{2}, b=\dfrac{3}{2}, c=\dfrac{3}{2}$.
Tổng $S=a+2b+3c=11$.
${{d}_{2}}$ đi qua điểm $B\left( 3;-1;2 \right)$ có $VTCP \overrightarrow{ {{u}_{2}}}=\left( 1;2;2 \right)$.
${{d}_{3}}$ đi qua điểm $C\left( 4;4;1 \right)$ có $VTCP \overrightarrow{{{u}_{3}}}=(2;-2;1)$.
Ta có: $\overrightarrow{{{u}_{1}}}.\overrightarrow{{{u}_{2}}}=0, \overrightarrow{{{u}_{2}}}.\overrightarrow{{{u}_{3}}}=0, \overrightarrow{{{u}_{3}}}.\overrightarrow{{{u}_{1}}}=0\Rightarrow \left( {{d}_{1}} \right),\left( {{d}_{2}} \right),\left( {{d}_{3}} \right)$ đôi một vuông góc với nhau.
$\left[ \overrightarrow{{{u}_{1}}}; \overrightarrow{{{u}_{2}}} \right].\overrightarrow{AB}\ne 0,\left[ \overrightarrow{{{u}_{2}}}; \overrightarrow{{{u}_{3}}} \right].\overrightarrow{BC}\ne 0,\left[ \overrightarrow{{{u}_{3}}},\overrightarrow{{{u}_{1}}} \right].\overrightarrow{CA}\ne 0\Rightarrow \left( {{d}_{1}} \right),\left( {{d}_{2}} \right),\left( {{d}_{3}} \right)$ đôi một chéo nhau.
Lại có: $\overrightarrow{AB}=\left( 2;-2;1 \right);\overrightarrow{AB}.\overrightarrow{ {{u}_{1}}}=0$ và $\overrightarrow{AB}. \overrightarrow{{{u}_{2}}}=0$ nên ${\left(d_{1}\right),\left(d_{2}\right),\left(d_{3}\right)}$ chứa 3 cạnh của hình hộp chữ nhật như hình vẽ.
${R=d\left(I, d_{1}\right)=d\left(I, d_{2}\right)=d\left(I, d_{3}\right) \Leftrightarrow R^{2}=d^{2}\left(I, d_{1}\right)=d^{2}\left(I, d_{2}\right)=d^{2}\left(I, d_{3}\right)}$ $\Leftrightarrow {{R}^{2}}={{\left( \dfrac{\left| \left[ \overrightarrow{AI},{{{\vec{u}}}_{1}} \right] \right|}{\left| \overrightarrow{{{u}_{1}}} \right|} \right)}^{2}}={{\left( \dfrac{\left| \left[ \overrightarrow{BI},\overrightarrow{{{u}_{2}}} \right] \right|}{\left| \overrightarrow{{{u}_{2}}} \right|} \right)}^{2}}={{\left( \dfrac{\left| \left[ \overrightarrow{CI},\overrightarrow{{{u}_{3}}} \right] \right|}{\left| \overline{{{u}_{3}}} \right|} \right)}^{2}}$, ta thấy ${{\left| \overrightarrow{{{u}_{1}}} \right|}^{2}}={{\left| \overrightarrow{{{u}_{2}}} \right|}^{2}}={{\left| \overrightarrow{{{u}_{3}}} \right|}^{2}}=9$ và
$\overrightarrow{AI}=\left( a-1;b-1;c-1 \right),\left[ \overrightarrow{AI},\overrightarrow{{{u}_{1}}} \right]=\left( -2b-c+3;2a+2c-4;a-2b+1 \right)$.
$\overrightarrow{BI}=\left( a-3;b+1;c-2 \right), \left[ \overrightarrow{BI},\overrightarrow{{{u}_{2}}} \right]=\left( 2b-2c+6;-2a+c+4;2a-b-7 \right).$ ${}$
$\overrightarrow{CI}=\left( a-4;b-4;c-1 \right),\left[ \overrightarrow{CI},\overrightarrow{{{u}_{3}}} \right]=\left( b+2c-6;-a+2c+2;-2a-2b+16 \right).$
$9{{R}^{2}}={{\left| \left[ \overrightarrow{AI},{{{\vec{u}}}_{1}} \right] \right|}^{2}}={{\left| \left[ \overrightarrow{BI},\overrightarrow{{{u}_{2}}} \right] \right|}^{2}}={{\left| \left[ \overrightarrow{CI},\overrightarrow{{{u}_{3}}} \right] \right|}^{2}}\Rightarrow 27{{R}^{2}}={{\left| \left[ \overrightarrow{AI},{{{\vec{u}}}_{1}} \right] \right|}^{2}}+{{\left| \left[ \overrightarrow{BI},\overrightarrow{{{u}_{2}}} \right] \right|}^{2}}+{{\left| \left[ \overrightarrow{CI},\overrightarrow{{{u}_{3}}} \right] \right|}^{2}}$
$=18\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)-126a-54b-54c+423=18{{\left( a-\dfrac{7}{2} \right)}^{2}}+18{{\left( b-\dfrac{3}{2} \right)}^{2}}+18{{\left( c-\dfrac{3}{2} \right)}^{2}}+\dfrac{243}{2}\ge \dfrac{243}{2}$ $\Rightarrow {{R}_{\min }}=\dfrac{3\sqrt{2}}{2}\approx 2,12$ khi $a=\dfrac{7}{2}, b=\dfrac{3}{2}, c=\dfrac{3}{2}$.
Tổng $S=a+2b+3c=11$.
Đáp án A.