Google
Câu hỏi: Trong không gian $Oxyz$, cho $A\left( 0;0;1 \right), B\left( 0;0;9 \right)$ và điểm $Q\left( 3;4;6 \right)$. Xét các điểm $M$ sao cho tam giác $MAB$ vuông tại $M$ và có diện tích lớn nhất. Giá trị nhỏ nhất của độ dài đoạn $MQ$ thuộc khoảng nào dưới đây?
A. $\left( 2;3 \right)$.
B. $\left( 4;5 \right)$.
C. $\left( 1;2 \right)$.
D. $\left( 3;4 \right)$.
A. $\left( 2;3 \right)$.
B. $\left( 4;5 \right)$.
C. $\left( 1;2 \right)$.
D. $\left( 3;4 \right)$.
Vì tam giác $MAB$ vuông tại $M$ nên điểm $M$ thuộc mặt cầu đường kính $AB$ (không trùng với $A, B$ ).
Trung điểm của $AB$ là $I\left( 0;0;5 \right)$ ; $R=\dfrac{AB}{2}=4\Rightarrow \left( S \right):{{x}^{2}}+{{y}^{2}}+{{\left( z-5 \right)}^{2}}=16$.
Tam giác $MAB$ có diện tích lớn nhất khi và chỉ khi $M$ thuộc đường tròn lớn là giao của mặt cầu với mặt phẳng trung trực của $AB$.
Mặt phẳng trung trực của $AB$ có phương trình $\left( P \right):z-5=0$.
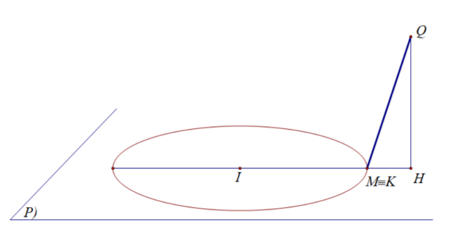Gọi $H$ là hình chiếu của $Q$ lên $\left( P \right)\Rightarrow H\left( 3;4;5 \right)\Rightarrow IH=5\Rightarrow H$ nằm ngoài đường tròn trên.
Gọi $K$ là giao của $IH$ với đường tròn( $K$ nằm giữa $H$ và $I$ ) $\Rightarrow HK=IH-R=1$.
Ta có $MQ=\sqrt{Q{{H}^{2}}+M{{H}^{2}}}\ge \sqrt{Q{{H}^{2}}+K{{H}^{2}}}=\sqrt{1+1}=\sqrt{2}\in \left( 1;2 \right)$.
Trung điểm của $AB$ là $I\left( 0;0;5 \right)$ ; $R=\dfrac{AB}{2}=4\Rightarrow \left( S \right):{{x}^{2}}+{{y}^{2}}+{{\left( z-5 \right)}^{2}}=16$.
Tam giác $MAB$ có diện tích lớn nhất khi và chỉ khi $M$ thuộc đường tròn lớn là giao của mặt cầu với mặt phẳng trung trực của $AB$.
Mặt phẳng trung trực của $AB$ có phương trình $\left( P \right):z-5=0$.
Gọi $K$ là giao của $IH$ với đường tròn( $K$ nằm giữa $H$ và $I$ ) $\Rightarrow HK=IH-R=1$.
Ta có $MQ=\sqrt{Q{{H}^{2}}+M{{H}^{2}}}\ge \sqrt{Q{{H}^{2}}+K{{H}^{2}}}=\sqrt{1+1}=\sqrt{2}\in \left( 1;2 \right)$.
Đáp án C.
