Google
Câu hỏi: Trong không gian $O x y z$, cho mặt cầu $x^2+y^2+z^2=9$ và điểm $M\left(x_0 ; y_0 ; z_0\right) \in d:\left\{\begin{array}{l}x=1+t \\ y=1+2 t \\ z=2-3 t\end{array}\right.$. Ba điểm $A, B, C$ phân biệt cùng thuộc mặt cầu sao cho $M A, M B, M C$ là tiếp tuyến của mặt cầu. Biết rằng mặt phẳng $(A B C)$ đi qua điểm $D(1 ; 1 ; 2)$. Tổng $T=x_0^2+y_0^2+z_0^2$ bằng
A. 21 .
B. 30 .
C. 26 .
D. 20 .
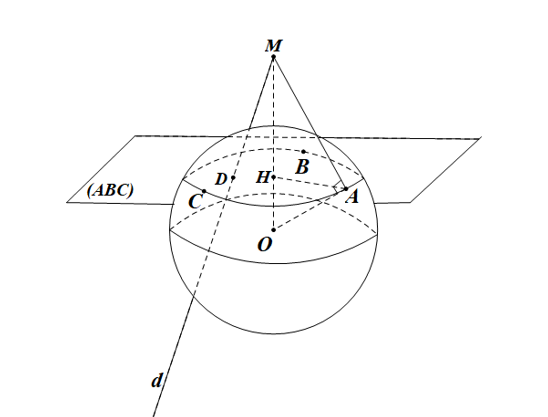* Mặt cầu có phương trình $x^2+y^2+z^2=9 \Rightarrow$ tâm $O(0 ; 0 ; 0)$, bán kính $R=3$.
* $M A, M B, M C$ là tiếp tuyến của mặt cầu $\Rightarrow M O \perp(A B C)$.
$\Rightarrow(A B C)$ đi qua $D(1 ; 1 ; 2)$ có véc tơ pháp tuyến $\overrightarrow{O M}\left(x_0 ; y_0 ; z_0\right)$ có phương trình dạng: ${{x}_{0}}\left( x-1 \right)+{{y}_{0}}\left( y-1 \right)+{{z}_{0}}\left( z-2 \right)=0$
MA là tiếp tuyến của mặt cầu tại A $\Rightarrow \Delta MOAvuongtaiA\Rightarrow OH.OM=O{{A}^{2}}={{R}^{2}}=9$
Gọi $H$ là hình chiếu của $O$ lên $(A B C)(O H+O M=H M)$, ta có:
$
\begin{aligned}
& d(O ;(A B C))=O H=\dfrac{\left|-x_0-y_0-2 z_0\right|}{\sqrt{x_0^2+y_0^2+z_0^2}}=\dfrac{\left|x_0+y_0+z_0+z_0\right|}{\sqrt{x_0^2+y_0^2+z_0^2}}=\dfrac{\left|z_0+4\right|}{O M} \Rightarrow O H . O M=\left|z_0+4\right| \\
& \Rightarrow\left|z_0+4\right|=9 \Leftrightarrow z_0=5 \vee z_0=-13 . \\
& * \mathrm{Với} z_0=5 \Rightarrow M(0 ;-1 ; 5) \Rightarrow T=26 \text { nhận do: } O M=\sqrt{26} ; O H=\dfrac{\left|z_0+4\right|}{O M}=\dfrac{9}{\sqrt{26}} \\
& p t(A B C):-y+5 z-9=0 \Rightarrow M H=d(M ;(A B C))=\dfrac{17}{\sqrt{26}} . \\
& \Rightarrow O H+H M=O M \\
& * \mathrm{Với} z_0=-13 \Rightarrow M(6 ; 11 ;-13) \Rightarrow \operatorname{loại~do:OM=\sqrt {326};OH=\dfrac {9}{\sqrt {326}}} ; \\
& (A B C): 6 x+11 y-13 z+9=0 \Rightarrow M H=d(M ;(A B C))=\dfrac{335}{\sqrt{326}} . \\
& \Rightarrow O H+H M \neq O M .
\end{aligned}
$
A. 21 .
B. 30 .
C. 26 .
D. 20 .
* $M A, M B, M C$ là tiếp tuyến của mặt cầu $\Rightarrow M O \perp(A B C)$.
$\Rightarrow(A B C)$ đi qua $D(1 ; 1 ; 2)$ có véc tơ pháp tuyến $\overrightarrow{O M}\left(x_0 ; y_0 ; z_0\right)$ có phương trình dạng: ${{x}_{0}}\left( x-1 \right)+{{y}_{0}}\left( y-1 \right)+{{z}_{0}}\left( z-2 \right)=0$
MA là tiếp tuyến của mặt cầu tại A $\Rightarrow \Delta MOAvuongtaiA\Rightarrow OH.OM=O{{A}^{2}}={{R}^{2}}=9$
Gọi $H$ là hình chiếu của $O$ lên $(A B C)(O H+O M=H M)$, ta có:
$
\begin{aligned}
& d(O ;(A B C))=O H=\dfrac{\left|-x_0-y_0-2 z_0\right|}{\sqrt{x_0^2+y_0^2+z_0^2}}=\dfrac{\left|x_0+y_0+z_0+z_0\right|}{\sqrt{x_0^2+y_0^2+z_0^2}}=\dfrac{\left|z_0+4\right|}{O M} \Rightarrow O H . O M=\left|z_0+4\right| \\
& \Rightarrow\left|z_0+4\right|=9 \Leftrightarrow z_0=5 \vee z_0=-13 . \\
& * \mathrm{Với} z_0=5 \Rightarrow M(0 ;-1 ; 5) \Rightarrow T=26 \text { nhận do: } O M=\sqrt{26} ; O H=\dfrac{\left|z_0+4\right|}{O M}=\dfrac{9}{\sqrt{26}} \\
& p t(A B C):-y+5 z-9=0 \Rightarrow M H=d(M ;(A B C))=\dfrac{17}{\sqrt{26}} . \\
& \Rightarrow O H+H M=O M \\
& * \mathrm{Với} z_0=-13 \Rightarrow M(6 ; 11 ;-13) \Rightarrow \operatorname{loại~do:OM=\sqrt {326};OH=\dfrac {9}{\sqrt {326}}} ; \\
& (A B C): 6 x+11 y-13 z+9=0 \Rightarrow M H=d(M ;(A B C))=\dfrac{335}{\sqrt{326}} . \\
& \Rightarrow O H+H M \neq O M .
\end{aligned}
$
Đáp án C.