hoankuty
Ngố Design
Bài toán
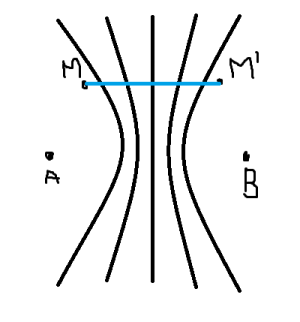
Tiến hành thực hiện giao thoa sóng nước với hai nguồn đồng bộ đặt tại hai điểm $A$ và $B$ cách nhau $20cm$. Phương trình dao động của nguồn là$u=2\cos \left(2\pi ft\right)\left(cm\right)$ (tần số $f$ thay đổi được) và tốc độ truyền sóng là $1,6 \ \left(\text{m}/\text{s}\right)$. M là một điểm trên mặt nước sao cho $MA=12\left(cm\right)$ và $MB=16\left(cm\right)$. Gọi số điểm dao động với biên độ cực đại trên đoạn $MA$ và $MB$ là $x$ và $y$. Khi $f=f_{0}$ hoặc $f=\dfrac{4}{3}f_{0}$ thì $y-x=5$. Khi $f=\dfrac{4}{3}\left(f_{0}+n\right)$ và ứng với giá trị $n$ nhỏ nhất bằng $6Hz$ thì $y-x\neq 5$. Gía trị $f_{0}$ gần với giá trị nào nhất sau đây?
A. $86Hz$
B. $84Hz$
C. $82Hz$
D. $88Hz$
Trích đề thi thử THPT Lần 3-Bamabel :)
P/s: thấy đáp án B. vừa xinh, đặt gạch hóng cao nhân ;)
Tiến hành thực hiện giao thoa sóng nước với hai nguồn đồng bộ đặt tại hai điểm $A$ và $B$ cách nhau $20cm$. Phương trình dao động của nguồn là$u=2\cos \left(2\pi ft\right)\left(cm\right)$ (tần số $f$ thay đổi được) và tốc độ truyền sóng là $1,6 \ \left(\text{m}/\text{s}\right)$. M là một điểm trên mặt nước sao cho $MA=12\left(cm\right)$ và $MB=16\left(cm\right)$. Gọi số điểm dao động với biên độ cực đại trên đoạn $MA$ và $MB$ là $x$ và $y$. Khi $f=f_{0}$ hoặc $f=\dfrac{4}{3}f_{0}$ thì $y-x=5$. Khi $f=\dfrac{4}{3}\left(f_{0}+n\right)$ và ứng với giá trị $n$ nhỏ nhất bằng $6Hz$ thì $y-x\neq 5$. Gía trị $f_{0}$ gần với giá trị nào nhất sau đây?
A. $86Hz$
B. $84Hz$
C. $82Hz$
D. $88Hz$
Trích đề thi thử THPT Lần 3-Bamabel :)
P/s: thấy đáp án B. vừa xinh, đặt gạch hóng cao nhân ;)
Lần chỉnh sửa cuối bởi 1 quản trị viên: