Giả sử ${{z}_{1}};{{z}_{2}}$ là hai trong số các số phức $z$ thoả...

Gọi $A,B$ là các điểm biểu diễn cho ${{z}_{2}};{{z}_{1}}$
Đặt $z=a+bi\Rightarrow \left( z-6 \right)\left( 8-i.\overline{z} \right)=\left[ \left( a-6 \right)+bi \right].\left[ \left( 8-b \right)-ai \right]$
Do $\left( z-6 \right)\left( 8-i.\overline{z} \right)$ là một số thực nên $-a.\left( a-6 \right)+b\left( 8-b \right)=0\Leftrightarrow {{a}^{2}}+{{b}^{2}}-6a-8b=0$
Suy ra $A,B$ thuộc đường tròn tâm $I\left( 3;4 \right)$, bán kính $R=5$
Gọi $M$ điểm thoả mãn $3\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}$.
Gọi $H$ là trung điểm của $AB$
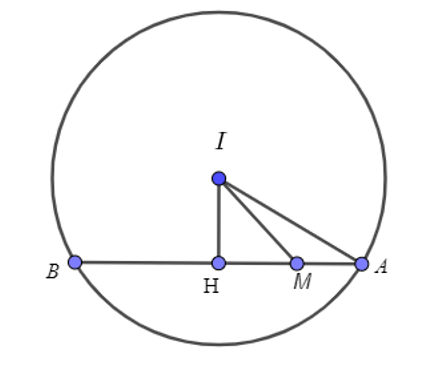Ta có $IH=\sqrt{I{{A}^{2}}-A{{H}^{2}}}=\sqrt{{{5}^{2}}-{{3}^{2}}}=4$ ; $IM=\sqrt{I{{H}^{2}}+M{{H}^{2}}}=\sqrt{{{4}^{2}}+{{\left( \dfrac{3}{2} \right)}^{2}}}=\dfrac{\sqrt{73}}{2}$.
Khi đó $M$ thuộc đường tròm tâm $I$, bán kính ${R}'=\dfrac{\sqrt{73}}{2}$.
Xét biểu thức $\left| {{z}_{1}}+3{{z}_{2}} \right|=\left| 3\overrightarrow{OA}+\overrightarrow{OB} \right|=\left| 4\overrightarrow{OM}+3\overrightarrow{MA}+\overleftarrow{MB} \right|=4OM$.
Ta có ${{\left| {{z}_{1}}+3{{z}_{2}} \right|}_{\min }}\Leftrightarrow O{{M}_{\min }}=\left| OI-{R}' \right|=5-\dfrac{\sqrt{73}}{2}$.
Vậy ${{\left| {{z}_{1}}+3{{z}_{2}} \right|}_{\min }}=4\left( 5-\dfrac{\sqrt{73}}{2} \right)=20-2\sqrt{73}$.