Có tất cả bao nhiêu giá trị nguyên của $y$ sao cho tương ứng với...

Đặt $f(x)=\log _{2020}\left(x+y^2\right)+\log _{2021}\left(y^2+y+64\right)-\log _4(x-y)$ (coi $y$ là tham số).
Điều kiện xác định của $f(x)$ là: $\left\{\begin{array}{l}x+y^2>0 \\ x-y>0\end{array} \Rightarrow x>y \geq-y^2\right.$ (do $x, y$ nguyên).
Do $x, y$ nguyên nên ta xét $f(x)$ trên nữa khoảng $[y+1 ;+\infty)$. Ta có:
$f^{\prime}(x)=\dfrac{1}{\left(x+y^2\right) \ln 2020}-\dfrac{1}{(x-y) \ln 4}<0, \forall x \geq y+1$.
Bảng biến thiên của $f(x)$ :
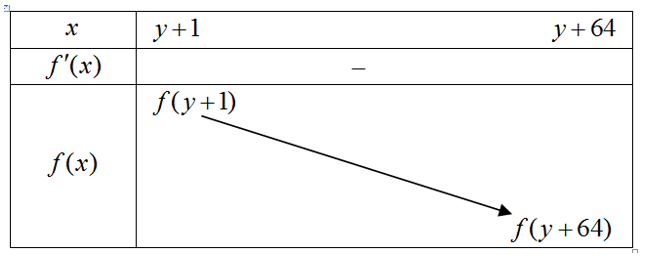Yêu cầu bài toán trở thành:
$
\begin{aligned}
& f(y+64)<0 \Leftrightarrow \log _{2020}\left(y^2+y+64\right)+\log _{2021}\left(y^2+y+64\right)<\log _4 64 \\
& \Leftrightarrow \log _{2021}\left(y^2+y+64\right)\left(\log _{2020} 2021+1\right)<3 \\
& \Leftrightarrow y^2+y+64-2021^{\dfrac{3}{\log _{2020^{2021+1}}}}<0 \Rightarrow-301,76<y<300,76 \text {. } \\
&
\end{aligned}
$
Vì $y \in \mathbb{Z}$ nên $y \in\{-301 ;-300 ; \ldots ; 299 ; 300\}$. Vậy có 602 giá trị nguyên của $y$ thỏa mãn yêu cầu bài toán.