Có bao nhiêu số nguyên $x,\left( x\ge -20 \right)$ sao cho ứng với...

Nhận xét $z=0$ ta được ${{\log }_{2}}2{{y}^{2}}={{\log }_{3}}{{y}^{3}}=x$, dẫn đến $y=x$, do đó mỗi giá trị $x$ chỉ tồn tại một cặp số thực $\left( x;0 \right)$ thỏa mãn, suy ra $z=0$ loại.
Với $z\ne 0$, ta có
${{\log }_{2}}\left( 2{{y}^{2}}+{{z}^{2}} \right)={{\log }_{3}}\left( {{y}^{3}}+2{{z}^{3}} \right)=x$
Ta có $\left\{ \begin{aligned}
& 2{{y}^{2}}+{{z}^{2}}={{2}^{x}} \\
& {{y}^{3}}+2{{z}^{3}}={{3}^{x}} \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& {{\left( 2{{y}^{2}}+{{z}^{2}} \right)}^{3}}={{8}^{x}} \\
& {{\left( {{y}^{3}}+2{{z}^{3}} \right)}^{2}}={{9}^{x}} \\
\end{aligned} \right.\Rightarrow \dfrac{{{\left( 2{{y}^{2}}+{{z}^{2}} \right)}^{3}}}{{{\left( {{y}^{3}}+2{{z}^{3}} \right)}^{2}}}={{\left( \dfrac{8}{9} \right)}^{x}}$
Mặt khác, $\dfrac{{{\left( 2{{y}^{2}}+{{z}^{2}} \right)}^{3}}}{{{\left( {{y}^{3}}+2{{z}^{3}} \right)}^{2}}}=\dfrac{{{\left[ 2{{\left( \dfrac{y}{z} \right)}^{2}}+1 \right]}^{3}}}{{{\left[ {{\left( \dfrac{y}{z} \right)}^{3}}+2 \right]}^{2}}}=\dfrac{{{\left( 2{{t}^{2}}+1 \right)}^{3}}}{{{\left( {{t}^{3}}+2 \right)}^{2}}}=f\left( t \right), t=\dfrac{y}{z}$.
Ta xét phương trình $f\left( t \right)={{\left( \dfrac{8}{9} \right)}^{x}}$
Ta có ${f}'\left( t \right)=\dfrac{12t{{\left( 2{{t}^{2}}+1 \right)}^{2}}{{\left( {{t}^{3}}+2 \right)}^{2}}-6{{t}^{2}}\left( {{t}^{3}}+2 \right){{\left( 2{{t}^{2}}+1 \right)}^{3}}}{{{\left( {{t}^{3}}+2 \right)}^{4}}}=\dfrac{6t{{\left( 2{{t}^{2}}+1 \right)}^{2}}\left( 4-t \right)}{{{\left( {{t}^{3}}+2 \right)}^{3}}}$
Ta xét ${f}'\left( t \right)=0$ tại $t=0,t=4$ và ${f}'\left( t \right)$ không xác định tại $t=-\sqrt[3]{2}$
Ta có bảng biến thiên của hàm số $y=f\left( t \right)$ như sau
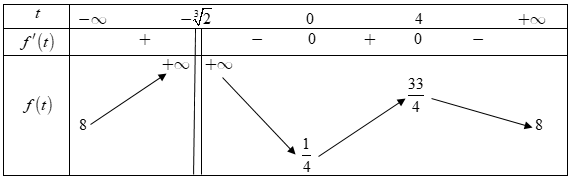Dựa vào bảng biến thiên để cho ứng với mỗi $x$ tồn tại đúng hai cặp số thực $\left( y,z \right)$, khi và chỉ khi $f\left( t \right)={{\left( \dfrac{8}{9} \right)}^{x}}$ có hai nghiệm phân biệt $t$ vì $t=\dfrac{y}{z}$.
$\begin{aligned}
& \Rightarrow \left\{ \begin{aligned}
& \left[ \begin{aligned}
& \dfrac{1}{4}<{{\left( \dfrac{8}{9} \right)}^{x}}\le 8 \\
& {{\left( \dfrac{8}{9} \right)}^{x}}>\dfrac{33}{4} \\
\end{aligned} \right. \\
& x\ge -20,x\in Z \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& \left[ \begin{aligned}
& {{\log }_{\dfrac{8}{9}}}\left( 8 \right)\le x<{{\log }_{\dfrac{8}{9}}}\left( \dfrac{1}{4} \right) \\
& x<{{\log }_{\dfrac{8}{9}}}\left( \dfrac{33}{4} \right) \\
\end{aligned} \right. \\
& x\ge -20,x\in Z \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& \left[ \begin{aligned}
& -17,65\le x<11,76 \\
& x<-17,91 \\
\end{aligned} \right. \\
& x\ge -20,x\in Z \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& \left[ \begin{aligned}
& -17,65\le x<11,76 \\
& -20\le x<-17,91 \\
\end{aligned} \right. \\
& x\in Z \\
\end{aligned} \right. \\
& \Rightarrow x\in \left[ -20,11 \right] \\
\end{aligned} $Vậy có 32 số nguyên $ x$ thỏa mãn yêu cầu đề bài.