Câu hỏi: Cho ${{z}_{1}};{{z}_{2}}$ là các số phức thỏa mãn $\left| {{z}_{1}} \right|=2;\left| {{z}_{2}} \right|=3$ và ${{z}_{1}}.\overline{{{z}_{2}}}$ là số thuần ảo. Giá trị lớn nhất của $P=\left| 4{{z}_{1}}-3{{z}_{2}}+1-2i \right|$ bằng
A. $15+\sqrt{5}.$
B. $5+\sqrt{5}.$
C. $\sqrt{65}+\sqrt{5}.$
D. $\sqrt{145}+\sqrt{5}.$
A. $15+\sqrt{5}.$
B. $5+\sqrt{5}.$
C. $\sqrt{65}+\sqrt{5}.$
D. $\sqrt{145}+\sqrt{5}.$
Gọi: ${{z}_{1}}=a+bi$ và $M\left( a;b \right)$ là điểm biểu diễn số phức ${{z}_{1}}$ $\Rightarrow \overrightarrow{OM}\left( a;b \right); OM=2$.
Gọi ${{z}_{2}}=c+di\Rightarrow \overline{{{z}_{2}}}=c-di$ và $N\left( c;d \right)$ là điểm biểu diễn số phức ${{z}_{2}}$ $\Rightarrow \overrightarrow{ON}\left( c;d \right); ON=3$.
Ta có ${{z}_{1}}.\overline{{{z}_{2}}}$ là số thuần ảo nên $ac+bd=0$, suy ra $\overrightarrow{OM}\bot \overrightarrow{ON}$ hay $\overrightarrow{OM}.\overrightarrow{ON}=0$.
Mà ${{\left| 4{{z}_{1}}-3{{z}_{2}} \right|}^{2}}={{\left| 4\overrightarrow{OM}-3\overrightarrow{ON} \right|}^{2}}=16{{\overrightarrow{OM}}^{2}}-24\overrightarrow{OM}.\overrightarrow{ON}+9{{\overrightarrow{ON}}^{2}}=16O{{M}^{2}}+9O{{N}^{2}}=145$.
Từ đó $\left| 4{{z}_{1}}-3{{z}_{2}} \right|=\sqrt{145}$. Xét $P=\left| 4{{z}_{1}}-3{{z}_{2}}+1-2i \right|\le \left| 4{{z}_{1}}-3{{z}_{2}} \right|+\left| 1-2i \right|=\sqrt{145}+\sqrt{5}$.
Dấu $''=''$ xảy ra khi $\left\{ \begin{aligned}
& 4{{z}_{1}}-3{{z}_{2}}=k\left( 1-2i \right),k\ge 0(1) \\
& \left| {{z}_{1}} \right|=2, \left| {{z}_{2}} \right|=3(2) \\
& ac+bd=0(3) \\
& \left| 4{{z}_{1}}-3{{z}_{2}} \right|=\sqrt{145}(4) \\
\end{aligned} \right.$.
Nhận xét:
Việc giải cụ thể hệ trên rất khó khăn, nên ta sẽ chỉ ra hệ trên có nghiệm $\left( {{z}_{1}}, {{z}_{2}} \right)$.
Lấy môđun 2 vế ở phương trình và sử dụng ta được $\left| k \right|=\sqrt{29}\Rightarrow k=\sqrt{29}$, do đó hệ tương đương với $\left\{ \begin{aligned}
& 4{{z}_{1}}-3{{z}_{2}}=\sqrt{29}\left( 1-2i \right),k\ge 0 \\
& \left| {{z}_{1}} \right|=2, \left| {{z}_{2}} \right|=3 \\
\end{aligned} \right.$.
Gọi $P, Q$ tương ứng là điểm biểu diễn $4{{z}_{1}}, 3{{z}_{2}}$ thì $\left\{ \begin{aligned}
& \overrightarrow{QP}=\left( \sqrt{29} ; -2\sqrt{29} \right) \\
& OP=8, OQ=9 \\
\end{aligned} \right.$.
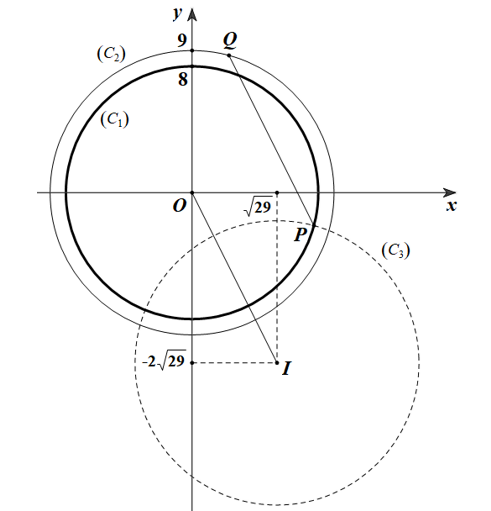 Gọi $\left( {{C}_{1}} \right)$ là đường tròn tâm $O$ bán kính ${{R}_{1}}=8$.
Gọi $\left( {{C}_{1}} \right)$ là đường tròn tâm $O$ bán kính ${{R}_{1}}=8$.
$\left( {{C}_{2}} \right)$ là đường tròn tâm $O$ bán kính ${{R}_{2}}=9$.
$\left( {{C}_{3}} \right)$ là ảnh của $\left( {{C}_{2}} \right)$ qua phép tịnh tiến $\overrightarrow{v}=\left( \sqrt{29} ; -2\sqrt{29} \right)$.
Khi đó $\left( {{C}_{3}} \right)$ có tâm $I\left( \sqrt{29} ; -2\sqrt{29} \right)$, bán kính ${{R}_{3}}=9$.
Có $OI=\sqrt{145}$ nên $\left| {{R}_{1}}-{{R}_{3}} \right|<OI<{{R}_{1}}+{{R}_{3}}$, do đó đường tròn $\left( {{C}_{3}} \right)$ sẽ cắt đường tròn $\left( {{C}_{1}} \right)$ tại 2 điểm phân biệt. Chọn $P$ là điểm tùy ý trong 2 điểm đó.
Khi đó $P\in \left( {{C}_{3}} \right)$ nên theo tính chất phép tịnh tiến $\exists Q\in \left( {{C}_{1}} \right)$ sao cho $\overrightarrow{QP}=\overrightarrow{v}=\left( \sqrt{29} ; -2\sqrt{29} \right)$.
Lại có $P\in \left( {{C}_{1}} \right)$ và $Q\in \left( {{C}_{2}} \right)$ nên $OP=8, OQ=9$.
Tóm lại tồn tại các điểm $P, Q$ sao cho hệ xảy ra, dẫn tới tồn tại ${{z}_{1}}, {{z}_{2}}$ sao cho đẳng thức $P=\sqrt{145}+\sqrt{5}$ xảy ra. Vậy $\max P=\sqrt{145}+\sqrt{5}$.
Gọi ${{z}_{2}}=c+di\Rightarrow \overline{{{z}_{2}}}=c-di$ và $N\left( c;d \right)$ là điểm biểu diễn số phức ${{z}_{2}}$ $\Rightarrow \overrightarrow{ON}\left( c;d \right); ON=3$.
Ta có ${{z}_{1}}.\overline{{{z}_{2}}}$ là số thuần ảo nên $ac+bd=0$, suy ra $\overrightarrow{OM}\bot \overrightarrow{ON}$ hay $\overrightarrow{OM}.\overrightarrow{ON}=0$.
Mà ${{\left| 4{{z}_{1}}-3{{z}_{2}} \right|}^{2}}={{\left| 4\overrightarrow{OM}-3\overrightarrow{ON} \right|}^{2}}=16{{\overrightarrow{OM}}^{2}}-24\overrightarrow{OM}.\overrightarrow{ON}+9{{\overrightarrow{ON}}^{2}}=16O{{M}^{2}}+9O{{N}^{2}}=145$.
Từ đó $\left| 4{{z}_{1}}-3{{z}_{2}} \right|=\sqrt{145}$. Xét $P=\left| 4{{z}_{1}}-3{{z}_{2}}+1-2i \right|\le \left| 4{{z}_{1}}-3{{z}_{2}} \right|+\left| 1-2i \right|=\sqrt{145}+\sqrt{5}$.
Dấu $''=''$ xảy ra khi $\left\{ \begin{aligned}
& 4{{z}_{1}}-3{{z}_{2}}=k\left( 1-2i \right),k\ge 0(1) \\
& \left| {{z}_{1}} \right|=2, \left| {{z}_{2}} \right|=3(2) \\
& ac+bd=0(3) \\
& \left| 4{{z}_{1}}-3{{z}_{2}} \right|=\sqrt{145}(4) \\
\end{aligned} \right.$.
Nhận xét:
Việc giải cụ thể hệ trên rất khó khăn, nên ta sẽ chỉ ra hệ trên có nghiệm $\left( {{z}_{1}}, {{z}_{2}} \right)$.
Lấy môđun 2 vế ở phương trình và sử dụng ta được $\left| k \right|=\sqrt{29}\Rightarrow k=\sqrt{29}$, do đó hệ tương đương với $\left\{ \begin{aligned}
& 4{{z}_{1}}-3{{z}_{2}}=\sqrt{29}\left( 1-2i \right),k\ge 0 \\
& \left| {{z}_{1}} \right|=2, \left| {{z}_{2}} \right|=3 \\
\end{aligned} \right.$.
Gọi $P, Q$ tương ứng là điểm biểu diễn $4{{z}_{1}}, 3{{z}_{2}}$ thì $\left\{ \begin{aligned}
& \overrightarrow{QP}=\left( \sqrt{29} ; -2\sqrt{29} \right) \\
& OP=8, OQ=9 \\
\end{aligned} \right.$.
$\left( {{C}_{2}} \right)$ là đường tròn tâm $O$ bán kính ${{R}_{2}}=9$.
$\left( {{C}_{3}} \right)$ là ảnh của $\left( {{C}_{2}} \right)$ qua phép tịnh tiến $\overrightarrow{v}=\left( \sqrt{29} ; -2\sqrt{29} \right)$.
Khi đó $\left( {{C}_{3}} \right)$ có tâm $I\left( \sqrt{29} ; -2\sqrt{29} \right)$, bán kính ${{R}_{3}}=9$.
Có $OI=\sqrt{145}$ nên $\left| {{R}_{1}}-{{R}_{3}} \right|<OI<{{R}_{1}}+{{R}_{3}}$, do đó đường tròn $\left( {{C}_{3}} \right)$ sẽ cắt đường tròn $\left( {{C}_{1}} \right)$ tại 2 điểm phân biệt. Chọn $P$ là điểm tùy ý trong 2 điểm đó.
Khi đó $P\in \left( {{C}_{3}} \right)$ nên theo tính chất phép tịnh tiến $\exists Q\in \left( {{C}_{1}} \right)$ sao cho $\overrightarrow{QP}=\overrightarrow{v}=\left( \sqrt{29} ; -2\sqrt{29} \right)$.
Lại có $P\in \left( {{C}_{1}} \right)$ và $Q\in \left( {{C}_{2}} \right)$ nên $OP=8, OQ=9$.
Tóm lại tồn tại các điểm $P, Q$ sao cho hệ xảy ra, dẫn tới tồn tại ${{z}_{1}}, {{z}_{2}}$ sao cho đẳng thức $P=\sqrt{145}+\sqrt{5}$ xảy ra. Vậy $\max P=\sqrt{145}+\sqrt{5}$.
Đáp án D.