Google
Câu hỏi: Cho lăng trụ đứng $ABC.{A}'{B}'{C}'$ có đáy ABC là tam giác vuông tại $A$. Khoảng cách từ đường thẳng $A{A}'$ đến mặt phẳng $\left( BC{C}'{B}' \right)$ bằng khoảng cách từ điểm $C$ đến mặt phẳng $\left( AB{C}' \right)$ và cùng bằng $1$. Góc giữa hai mặt phẳng $\left( AB{C}' \right)$ và $\left( ABC \right)$ bằng $\varphi $. Tính $\tan \varphi $ khi thể tích khối lăng trụ $ABC.{A}'{B}'{C}'$ nhỏ nhất.
A. $\tan \varphi =\sqrt{2}$.
B. $\tan \varphi =\dfrac{1}{\sqrt{3}}$.
C. $\tan \varphi =\sqrt{3}$.
D. $\tan \varphi =\dfrac{1}{\sqrt{2}}$.
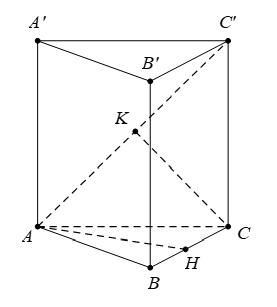Kẻ $AH\bot BC\Rightarrow AH\bot (BCC'B')$,
Vì $AA'\parallel \left( BCC'B' \right)\Rightarrow d\left( AA',(BCC'B') \right)=d\left( A,\left( BCC'B' \right) \right)=AH=1$.
Kẻ $CK\bot AC'$, vì $AB\bot AC$ và $AB\bot AA'\Rightarrow AB\bot \left( ACC'A' \right)\Rightarrow AB\bot CK$.
$\Rightarrow CK\bot \left( ABC' \right)\Rightarrow CK=d\left( C,\left( ABC' \right) \right)=1$.
Ta có $AB\bot \left( ACC'A' \right)\Rightarrow \widehat{CAC'}$ là góc giữa hai mặt phẳng $\left( ABC' \right)$ và $\left( ABC \right)$
Suy ra $\widehat{CAC'}=\varphi $. Do $AC=\dfrac{CK}{\sin \varphi }=\dfrac{1}{\sin \varphi }$, $CC'=\dfrac{CK}{\cos \varphi }=\dfrac{1}{\cos \varphi }$.
$\dfrac{1}{A{{B}^{2}}}=\dfrac{1}{A{{H}^{2}}}-\dfrac{1}{A{{C}^{2}}}=1-{{\sin }^{2}}\varphi =\text{co}{{\text{s}}^{2}}\varphi $ $\Rightarrow AB=\dfrac{1}{\text{cos}\varphi }$.
${{S}_{\Delta ABC}}=\dfrac{1}{2}AB.AC=\dfrac{1}{2\sin \varphi \cos \varphi }$
(Bản word bạn đang sử dụng phát hành từ website Tailieuchuan.vn)
Thể tích lăng trụ $ABC.A'B'C'$ là $V=CC'.{{S}_{\Delta ABC}}$ $=\dfrac{1}{2\sin \varphi {{\cos }^{2}}\varphi }$.
Do ${{\left( \sin \varphi {{\cos }^{2}}\varphi \right)}^{2}}=\dfrac{1}{2}.2{{\sin }^{2}}\varphi .{{\cos }^{2}}\varphi .{{\cos }^{2}}\varphi \le \dfrac{1}{2}{{\left( \dfrac{2{{\sin }^{2}}\varphi +{{\cos }^{2}}\varphi +{{\cos }^{2}}\varphi }{3} \right)}^{3}}=\dfrac{4}{27}$.
$\Rightarrow \sin \varphi {{\cos }^{2}}\varphi \le \dfrac{2\sqrt{3}}{9}\Rightarrow V\ge \dfrac{3\sqrt{3}}{4}$.
Suy ra thể tích lăng trụ nhỏ nhất là $V=\dfrac{3\sqrt{3}}{4}$ khi $2{{\sin }^{2}}\varphi ={{\cos }^{2}}\varphi \Leftrightarrow {{\tan }^{2}}\varphi =\dfrac{1}{2}$ $\Rightarrow \tan \varphi =\dfrac{1}{\sqrt{2}}$.
A. $\tan \varphi =\sqrt{2}$.
B. $\tan \varphi =\dfrac{1}{\sqrt{3}}$.
C. $\tan \varphi =\sqrt{3}$.
D. $\tan \varphi =\dfrac{1}{\sqrt{2}}$.
Vì $AA'\parallel \left( BCC'B' \right)\Rightarrow d\left( AA',(BCC'B') \right)=d\left( A,\left( BCC'B' \right) \right)=AH=1$.
Kẻ $CK\bot AC'$, vì $AB\bot AC$ và $AB\bot AA'\Rightarrow AB\bot \left( ACC'A' \right)\Rightarrow AB\bot CK$.
$\Rightarrow CK\bot \left( ABC' \right)\Rightarrow CK=d\left( C,\left( ABC' \right) \right)=1$.
Ta có $AB\bot \left( ACC'A' \right)\Rightarrow \widehat{CAC'}$ là góc giữa hai mặt phẳng $\left( ABC' \right)$ và $\left( ABC \right)$
Suy ra $\widehat{CAC'}=\varphi $. Do $AC=\dfrac{CK}{\sin \varphi }=\dfrac{1}{\sin \varphi }$, $CC'=\dfrac{CK}{\cos \varphi }=\dfrac{1}{\cos \varphi }$.
$\dfrac{1}{A{{B}^{2}}}=\dfrac{1}{A{{H}^{2}}}-\dfrac{1}{A{{C}^{2}}}=1-{{\sin }^{2}}\varphi =\text{co}{{\text{s}}^{2}}\varphi $ $\Rightarrow AB=\dfrac{1}{\text{cos}\varphi }$.
${{S}_{\Delta ABC}}=\dfrac{1}{2}AB.AC=\dfrac{1}{2\sin \varphi \cos \varphi }$
(Bản word bạn đang sử dụng phát hành từ website Tailieuchuan.vn)
Thể tích lăng trụ $ABC.A'B'C'$ là $V=CC'.{{S}_{\Delta ABC}}$ $=\dfrac{1}{2\sin \varphi {{\cos }^{2}}\varphi }$.
Do ${{\left( \sin \varphi {{\cos }^{2}}\varphi \right)}^{2}}=\dfrac{1}{2}.2{{\sin }^{2}}\varphi .{{\cos }^{2}}\varphi .{{\cos }^{2}}\varphi \le \dfrac{1}{2}{{\left( \dfrac{2{{\sin }^{2}}\varphi +{{\cos }^{2}}\varphi +{{\cos }^{2}}\varphi }{3} \right)}^{3}}=\dfrac{4}{27}$.
$\Rightarrow \sin \varphi {{\cos }^{2}}\varphi \le \dfrac{2\sqrt{3}}{9}\Rightarrow V\ge \dfrac{3\sqrt{3}}{4}$.
Suy ra thể tích lăng trụ nhỏ nhất là $V=\dfrac{3\sqrt{3}}{4}$ khi $2{{\sin }^{2}}\varphi ={{\cos }^{2}}\varphi \Leftrightarrow {{\tan }^{2}}\varphi =\dfrac{1}{2}$ $\Rightarrow \tan \varphi =\dfrac{1}{\sqrt{2}}$.
Đáp án D.