Google
Câu hỏi: Cho hình nón tròn xoay có đường cao bằng $2a$. Một thiết diện đi qua đỉnh của hình nón có diện tích bằng $\dfrac{24{{a}^{2}}\sqrt{3}}{7}$ và khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện bằng $\dfrac{3a}{2}$. Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng:
A. $18\pi {{a}^{3}}$.
B. $4\pi {{a}^{3}}$.
C. $12\pi {{a}^{3}}.$
D. $6\pi {{a}^{3}}$.
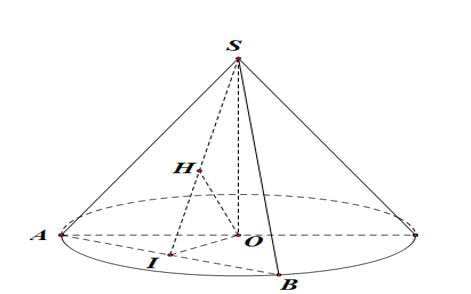Xét hình nón đỉnh $S$ có chiều cao $h=SO=2a$.
Thiết diện đi qua đỉnh của hình nón là tam giác $SAB$ cân tại $S$.
+ Gọi $I$ là trung điểm của đoạn thẳng $AB$. Trong tam giác $SOI$, kẻ $OH\bot SI$, $H\in SI$.
+ $\left\{ \begin{aligned}
& AB\bot OI \\
& AB\bot SO \\
\end{aligned} \right.\Rightarrow AB\bot \left( SOI \right)\Rightarrow AB\bot OH$.
+$\left\{ \begin{aligned}
& OH\bot SI \\
& OH\bot AB \\
\end{aligned} \right.$$\Rightarrow OH\bot \left( SAB \right) $ $ \Rightarrow d\left( O , \left( SAB \right) \right)=OH=\dfrac{3a}{2}$.
Xét tam giác $SOI$ vuông tại $O$, ta có $\dfrac{1}{O{{I}^{2}}}=\dfrac{1}{O{{H}^{2}}}-\dfrac{1}{S{{O}^{2}}}=\dfrac{4}{9{{a}^{2}}}-\dfrac{1}{4{{a}^{2}}}=\dfrac{7}{36{{a}^{2}}}$ $\Rightarrow OI=\dfrac{6a}{\sqrt{7}}$.
và $SI=\sqrt{O{{I}^{2}}+S{{O}^{2}}}=\sqrt{{{\left( \dfrac{6a}{\sqrt{7}} \right)}^{2}}+{{\left( 2a \right)}^{2}}}=\dfrac{8a\sqrt{7}}{7}$.
Ta có ${{S}_{\Delta SAB}}=\dfrac{24{{a}^{2}}\sqrt{3}}{7}\Leftrightarrow \dfrac{1}{2}SI.AB=\dfrac{24{{a}^{2}}\sqrt{3}}{7}\Rightarrow AB=\dfrac{6a\sqrt{21}}{7}\Rightarrow IA=\dfrac{AB}{2}=\dfrac{3a\sqrt{21}}{7}$
Xét tam giác $IAO$ vuông tại $I\Rightarrow R=OA=\sqrt{O{{I}^{2}}+I{{A}^{2}}}=\sqrt{{{\left( \dfrac{6a}{\sqrt{7}} \right)}^{2}}+{{\left( \dfrac{3a\sqrt{21}}{7} \right)}^{2}}}=3a$.
Thể tích của khối nón giới hạn bởi hình nón là: $V=\dfrac{1}{3}h.\pi {{R}^{2}}=\dfrac{1}{3}.2a.\pi .{{\left( 3a \right)}^{2}}=6\pi {{a}^{3}}.$
A. $18\pi {{a}^{3}}$.
B. $4\pi {{a}^{3}}$.
C. $12\pi {{a}^{3}}.$
D. $6\pi {{a}^{3}}$.
Thiết diện đi qua đỉnh của hình nón là tam giác $SAB$ cân tại $S$.
+ Gọi $I$ là trung điểm của đoạn thẳng $AB$. Trong tam giác $SOI$, kẻ $OH\bot SI$, $H\in SI$.
+ $\left\{ \begin{aligned}
& AB\bot OI \\
& AB\bot SO \\
\end{aligned} \right.\Rightarrow AB\bot \left( SOI \right)\Rightarrow AB\bot OH$.
+$\left\{ \begin{aligned}
& OH\bot SI \\
& OH\bot AB \\
\end{aligned} \right.$$\Rightarrow OH\bot \left( SAB \right) $ $ \Rightarrow d\left( O , \left( SAB \right) \right)=OH=\dfrac{3a}{2}$.
Xét tam giác $SOI$ vuông tại $O$, ta có $\dfrac{1}{O{{I}^{2}}}=\dfrac{1}{O{{H}^{2}}}-\dfrac{1}{S{{O}^{2}}}=\dfrac{4}{9{{a}^{2}}}-\dfrac{1}{4{{a}^{2}}}=\dfrac{7}{36{{a}^{2}}}$ $\Rightarrow OI=\dfrac{6a}{\sqrt{7}}$.
và $SI=\sqrt{O{{I}^{2}}+S{{O}^{2}}}=\sqrt{{{\left( \dfrac{6a}{\sqrt{7}} \right)}^{2}}+{{\left( 2a \right)}^{2}}}=\dfrac{8a\sqrt{7}}{7}$.
Ta có ${{S}_{\Delta SAB}}=\dfrac{24{{a}^{2}}\sqrt{3}}{7}\Leftrightarrow \dfrac{1}{2}SI.AB=\dfrac{24{{a}^{2}}\sqrt{3}}{7}\Rightarrow AB=\dfrac{6a\sqrt{21}}{7}\Rightarrow IA=\dfrac{AB}{2}=\dfrac{3a\sqrt{21}}{7}$
Xét tam giác $IAO$ vuông tại $I\Rightarrow R=OA=\sqrt{O{{I}^{2}}+I{{A}^{2}}}=\sqrt{{{\left( \dfrac{6a}{\sqrt{7}} \right)}^{2}}+{{\left( \dfrac{3a\sqrt{21}}{7} \right)}^{2}}}=3a$.
Thể tích của khối nón giới hạn bởi hình nón là: $V=\dfrac{1}{3}h.\pi {{R}^{2}}=\dfrac{1}{3}.2a.\pi .{{\left( 3a \right)}^{2}}=6\pi {{a}^{3}}.$
Đáp án D.
