Google
Câu hỏi: Cho hình nón đỉnh $S$, tâm mặt đáy $O$ và có diện tích xung quanh bằng $20\pi {{a}^{2}}$. Gọi $A$ và $B$ là hai điểm thuộc đường tròn đáy sao cho độ dài cung $\overset\frown{AB}$ bằng $\dfrac{1}{3}$ lần chu vi của đường tròn đáy. Biết rằng bán kính đáy bằng $4a$, khoảng cách từ $O$ đến mặt phẳng $\left( SAB \right)$ bằng
A. $\dfrac{2\sqrt{13}}{13}a$.
B. $\dfrac{\sqrt{13}}{13}a$.
C. $\dfrac{12\sqrt{13}}{13}a$.
D. $\dfrac{6\sqrt{13}}{13}a$.
Ta có ${{S}_{xq}}=\pi rl=20\pi {{a}^{2}}\Leftrightarrow \pi .4a.l=20\pi {{a}^{2}}\Leftrightarrow l=5a$.
$SO=\sqrt{S{{A}^{2}}-O{{A}^{2}}}=\sqrt{{{\left( 5a \right)}^{2}}-{{\left( 4a \right)}^{2}}}=3a$.
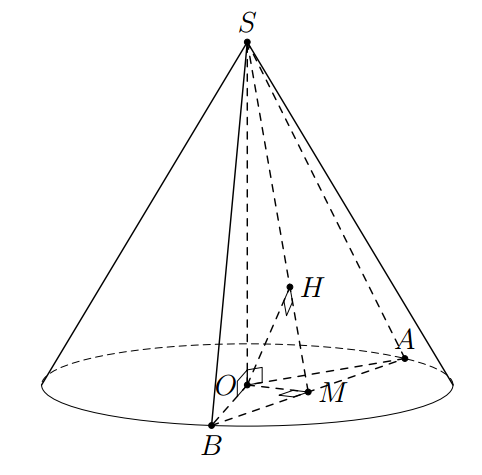
Gọi $M$ là trung điểm của đoạn thẳng $AB$. Khi đó $AB\bot \left( SOM \right)$. Gọi $H$ là hình chiếu vuông góc của $O$ lên $SM$. Suy ra $OH\bot \left( SAB \right)$ hay $d\left( O , \left( SAB \right) \right)=OH$.
Vì độ dài cung $\overset\frown{AB}$ bằng $\dfrac{1}{3}$ lần chu vi của đường tròn đáy nên góc $\widehat{AOB}=120{}^\circ \Rightarrow \widehat{MOB}=60{}^\circ $
Ta có $\cos \widehat{MOB}=\dfrac{OM}{OB}\Rightarrow OM=OB.\cos \widehat{MOB}=4a.\cos 60{}^\circ =2a$.
Suy ra $\dfrac{1}{O{{H}^{2}}}=\dfrac{1}{O{{M}^{2}}}+\dfrac{1}{O{{S}^{2}}}\Leftrightarrow \dfrac{1}{O{{H}^{2}}}=\dfrac{1}{{{\left( 2a \right)}^{2}}}+\dfrac{1}{{{\left( 3a \right)}^{2}}}\Leftrightarrow OH=\dfrac{6\sqrt{13}}{13}a$.
A. $\dfrac{2\sqrt{13}}{13}a$.
B. $\dfrac{\sqrt{13}}{13}a$.
C. $\dfrac{12\sqrt{13}}{13}a$.
D. $\dfrac{6\sqrt{13}}{13}a$.
$SO=\sqrt{S{{A}^{2}}-O{{A}^{2}}}=\sqrt{{{\left( 5a \right)}^{2}}-{{\left( 4a \right)}^{2}}}=3a$.
Gọi $M$ là trung điểm của đoạn thẳng $AB$. Khi đó $AB\bot \left( SOM \right)$. Gọi $H$ là hình chiếu vuông góc của $O$ lên $SM$. Suy ra $OH\bot \left( SAB \right)$ hay $d\left( O , \left( SAB \right) \right)=OH$.
Vì độ dài cung $\overset\frown{AB}$ bằng $\dfrac{1}{3}$ lần chu vi của đường tròn đáy nên góc $\widehat{AOB}=120{}^\circ \Rightarrow \widehat{MOB}=60{}^\circ $
Ta có $\cos \widehat{MOB}=\dfrac{OM}{OB}\Rightarrow OM=OB.\cos \widehat{MOB}=4a.\cos 60{}^\circ =2a$.
Suy ra $\dfrac{1}{O{{H}^{2}}}=\dfrac{1}{O{{M}^{2}}}+\dfrac{1}{O{{S}^{2}}}\Leftrightarrow \dfrac{1}{O{{H}^{2}}}=\dfrac{1}{{{\left( 2a \right)}^{2}}}+\dfrac{1}{{{\left( 3a \right)}^{2}}}\Leftrightarrow OH=\dfrac{6\sqrt{13}}{13}a$.
Đáp án D.
