Google
Câu hỏi: Cho hình chóp tứ giác đều $S.ABCD$ có $ABCD$ là hình vuông tâm $O$, cạnh bằng $4a$, góc giữa mặt bên và mặt đáy bằng ${{45}^{0}}$. Gọi $M$ là trung điểm $AD$, $H, K$ lần lượt là hai điểm thay đổi thuộc miền trong tam giác $SAB$ và $SCD$ sao cho $HK\parallel \left( ABCD \right)$, $SHOK$ là tứ giác nội tiếp. Tìm giá trị lớn nhất của thể tích khối chóp $M.SHOK.$
A. $4{{a}^{3}}$.
B. $\dfrac{4}{3}{{a}^{3}}$.
C. $\dfrac{16\sqrt{6}}{9}{{a}^{3}}$.
D. $\dfrac{2}{3}{{a}^{3}}$.
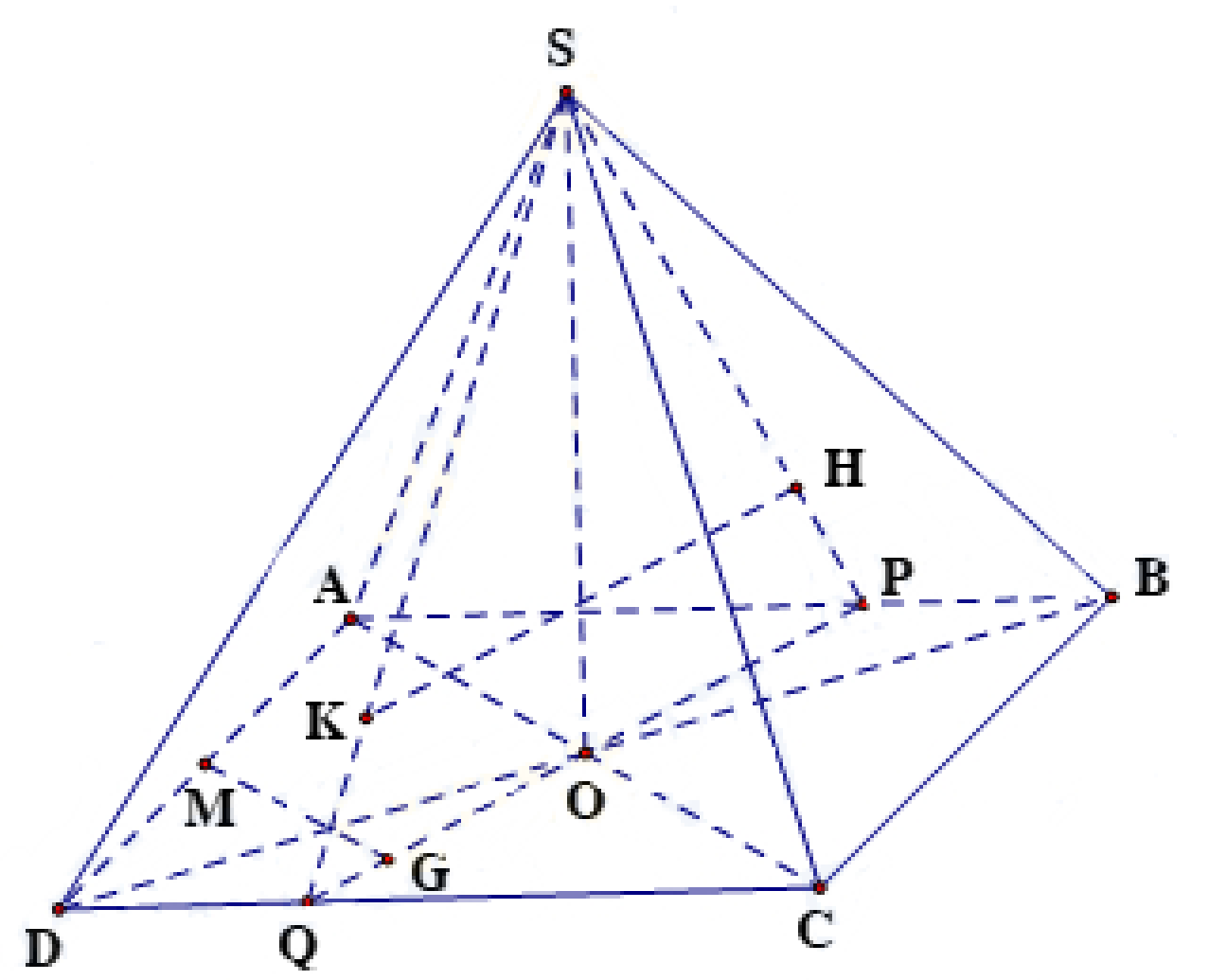Gọi $P, Q$ lần lượt là giao điểm của $SH$ với $AB$, $SK$ với $CD$, kẻ $MG\bot PQ$.
Vì $HK\parallel \left( ABCD \right), SO\bot \left( ABCD \right)$ nên $HK\bot SO$.
Do tính đối xứng nên $SO$ đi qua trung điểm của $HK$.
Mà $SHOK$ là tứ giác nội tiếp nên $SO$ là đường kính của đường tròn ngoại tiếp tứ giác $SHOK$.
Ta có: $\left( \left( SAD \right),\left( ABCD \right) \right)=\widehat{SMO}={{45}^{0}}$, $SO=2a$.
${{V}_{M.SHOK}}=\dfrac{1}{3}.MG.\dfrac{1}{2}.SO.HK=\dfrac{1}{6}.SO.MG.HK=\dfrac{a}{3}.MG.HK$.
Để ${{V}_{M.SHOK}}$ lớn nhất thì $MG.HK$ lớn nhất, khi và chỉ khi $HK$ là đường kính của đường tròn ngoại tiếp tứ giác $SHOK$ và $MG=MO$.
Vậy thể tích lớn nhất của khối chóp $M.SHOK$ là: $\dfrac{1}{6}.2a.2a.2a=\dfrac{4}{3}{{a}^{3}}$.
A. $4{{a}^{3}}$.
B. $\dfrac{4}{3}{{a}^{3}}$.
C. $\dfrac{16\sqrt{6}}{9}{{a}^{3}}$.
D. $\dfrac{2}{3}{{a}^{3}}$.
Vì $HK\parallel \left( ABCD \right), SO\bot \left( ABCD \right)$ nên $HK\bot SO$.
Do tính đối xứng nên $SO$ đi qua trung điểm của $HK$.
Mà $SHOK$ là tứ giác nội tiếp nên $SO$ là đường kính của đường tròn ngoại tiếp tứ giác $SHOK$.
Ta có: $\left( \left( SAD \right),\left( ABCD \right) \right)=\widehat{SMO}={{45}^{0}}$, $SO=2a$.
${{V}_{M.SHOK}}=\dfrac{1}{3}.MG.\dfrac{1}{2}.SO.HK=\dfrac{1}{6}.SO.MG.HK=\dfrac{a}{3}.MG.HK$.
Để ${{V}_{M.SHOK}}$ lớn nhất thì $MG.HK$ lớn nhất, khi và chỉ khi $HK$ là đường kính của đường tròn ngoại tiếp tứ giác $SHOK$ và $MG=MO$.
Vậy thể tích lớn nhất của khối chóp $M.SHOK$ là: $\dfrac{1}{6}.2a.2a.2a=\dfrac{4}{3}{{a}^{3}}$.
Đáp án B.
