Google
Câu hỏi: Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a\sqrt{3}$. Gọi $M,N$ lần lượt là trung điểm của $SB,SC$. Biết mặt phẳng $\left( AMN \right)$ vuông góc với mặt phẳng $\left( SBC \right)$. Tính thể tích của khối chóp $A.BCNM$.
A. $\dfrac{3{{a}^{3}}\sqrt{15}}{16}$.
B. $\dfrac{3{{a}^{3}}\sqrt{15}}{48}$.
C. $\dfrac{3{{a}^{3}}\sqrt{15}}{32}$.
D. $\dfrac{{{a}^{3}}\sqrt{15}}{32}$.
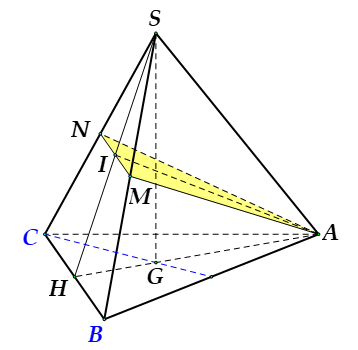Gọi $H$ là trung điểm $BC$ $\Rightarrow $ $BC\bot SH$ (do $\Delta SBC$ cân tại $S$ ).
Gọi $G$ là trọng tâm $\Delta ABC$ và $I=SH\cap MN$.
Do $S.ABC$ là chóp đều $\Rightarrow SG\bot \left( ABC \right)$.
Ta có: $MN$ là đường trung bình của $\Delta SBC\Rightarrow MN//BC\Rightarrow MN\bot SH$ tại $I$.
Vậy: $\left\{ \begin{aligned}
& \left( AMN \right)\bot \left( SBC \right) \\
& \left( AMN \right)\cap \left( SBC \right)=MN \\
& SH\bot MN,SH\subset \left( SBC \right) \\
\end{aligned} \right.\Rightarrow SH\bot \left( AMN \right)\Rightarrow SH\bot AI$.
Lại có $I$ là trung điểm $SH$ (do $I\in MN$ ) $\Rightarrow AI$ là đường trung tuyến $\Delta SAH$.
Suy ra $\Delta SAH$ cân tại $A\Rightarrow SA=AH=\dfrac{AB\sqrt{3}}{2}=\dfrac{3a}{2}$.
Xét $\Delta SGA$ vuông tại $G$ : $SG=\sqrt{S{{A}^{2}}-A{{G}^{2}}}=\sqrt{{{\left( \dfrac{3a}{2} \right)}^{2}}-{{\left( \dfrac{2}{3}.\dfrac{3a}{2} \right)}^{2}}}=\dfrac{a\sqrt{5}}{2}$.
Mặt khác: $\dfrac{{{V}_{S.AMN}}}{{{V}_{S.ABC}}}=\dfrac{SM}{SB}.\dfrac{SN}{SC}=\dfrac{1}{4}\Rightarrow {{V}_{MNABC}}=\dfrac{3}{4}{{V}_{S.ABC}}=\dfrac{3}{4}.\dfrac{1}{3}.SG.\dfrac{A{{B}^{2}}\sqrt{3}}{4}=\dfrac{3\sqrt{15}}{32}{{a}^{3}}$.
A. $\dfrac{3{{a}^{3}}\sqrt{15}}{16}$.
B. $\dfrac{3{{a}^{3}}\sqrt{15}}{48}$.
C. $\dfrac{3{{a}^{3}}\sqrt{15}}{32}$.
D. $\dfrac{{{a}^{3}}\sqrt{15}}{32}$.
Gọi $G$ là trọng tâm $\Delta ABC$ và $I=SH\cap MN$.
Do $S.ABC$ là chóp đều $\Rightarrow SG\bot \left( ABC \right)$.
Ta có: $MN$ là đường trung bình của $\Delta SBC\Rightarrow MN//BC\Rightarrow MN\bot SH$ tại $I$.
Vậy: $\left\{ \begin{aligned}
& \left( AMN \right)\bot \left( SBC \right) \\
& \left( AMN \right)\cap \left( SBC \right)=MN \\
& SH\bot MN,SH\subset \left( SBC \right) \\
\end{aligned} \right.\Rightarrow SH\bot \left( AMN \right)\Rightarrow SH\bot AI$.
Lại có $I$ là trung điểm $SH$ (do $I\in MN$ ) $\Rightarrow AI$ là đường trung tuyến $\Delta SAH$.
Suy ra $\Delta SAH$ cân tại $A\Rightarrow SA=AH=\dfrac{AB\sqrt{3}}{2}=\dfrac{3a}{2}$.
Xét $\Delta SGA$ vuông tại $G$ : $SG=\sqrt{S{{A}^{2}}-A{{G}^{2}}}=\sqrt{{{\left( \dfrac{3a}{2} \right)}^{2}}-{{\left( \dfrac{2}{3}.\dfrac{3a}{2} \right)}^{2}}}=\dfrac{a\sqrt{5}}{2}$.
Mặt khác: $\dfrac{{{V}_{S.AMN}}}{{{V}_{S.ABC}}}=\dfrac{SM}{SB}.\dfrac{SN}{SC}=\dfrac{1}{4}\Rightarrow {{V}_{MNABC}}=\dfrac{3}{4}{{V}_{S.ABC}}=\dfrac{3}{4}.\dfrac{1}{3}.SG.\dfrac{A{{B}^{2}}\sqrt{3}}{4}=\dfrac{3\sqrt{15}}{32}{{a}^{3}}$.
Đáp án C.