Google
Câu hỏi: Cho hình chóp $S.ABCD$ có đáy là hình chữ nhật, $AB=2a, AD=a$. Tam giác $SAB$ đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ $A$ đến mặt phẳng $\left( SBD \right)$ bằng
A. $\dfrac{2a\sqrt{5}}{3}$.
B. $\dfrac{a\sqrt{3}}{2}$.
C. $\dfrac{a\sqrt{5}}{5}$.
D. $\dfrac{a\sqrt{3}}{4}$.
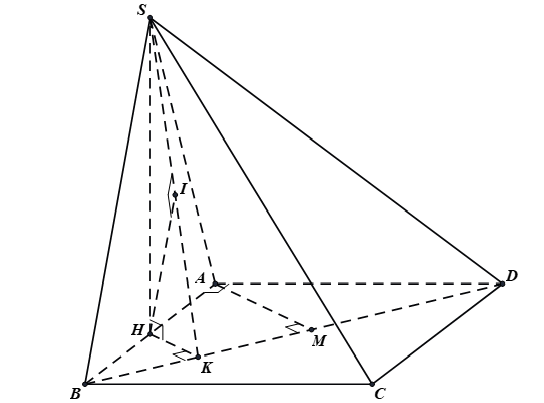Gọi $H$ là trung điểm $AB$, suy ra $SH\bot \left( ABCD \right)$.
Trong $\left( ABCD \right)$, dựng $AM\bot BD, HK\bot BD$ ; trong $\left( SHK \right)$, dựng $HI\bot SK$.
Ta có $\left\{ \begin{aligned}
& BD\bot HK \\
& BD\bot SH \\
\end{aligned} \right.\Rightarrow BD\bot \left( SHK \right)\Rightarrow BD\bot HI $, mà $ HI\bot SK $, suy ra $ HI\bot \left( SBD \right)$.
Khi đó, ta có $\text{d}\left( A ,\left( SBD \right) \right)=\text{d}\left( H,\left( SBD \right) \right).\dfrac{AB}{HB}=2HI$.
Trong $\Delta SAB$ đều, ta có $SH=AB\dfrac{\sqrt{3}}{2}=a\sqrt{3}$.
Trong $\Delta ABD$ vuông tại $A$, ta có $\dfrac{1}{A{{M}^{2}}}=\dfrac{1}{A{{B}^{2}}}+\dfrac{1}{A{{D}^{2}}}\Rightarrow AM=\dfrac{2a\sqrt{5}}{5}\Rightarrow HK=\dfrac{1}{2}AM=\dfrac{a\sqrt{5}}{5}$.
Trong $\Delta SHK$ vuông tại $H$, ta có $\dfrac{1}{H{{I}^{2}}}=\dfrac{1}{S{{H}^{2}}}+\dfrac{1}{H{{K}^{2}}}\Rightarrow HI=\dfrac{a\sqrt{3}}{4}$.
Vậy $\text{d}\left( A ,\left( SBD \right) \right)=\dfrac{a\sqrt{3}}{2}$.
A. $\dfrac{2a\sqrt{5}}{3}$.
B. $\dfrac{a\sqrt{3}}{2}$.
C. $\dfrac{a\sqrt{5}}{5}$.
D. $\dfrac{a\sqrt{3}}{4}$.
Trong $\left( ABCD \right)$, dựng $AM\bot BD, HK\bot BD$ ; trong $\left( SHK \right)$, dựng $HI\bot SK$.
Ta có $\left\{ \begin{aligned}
& BD\bot HK \\
& BD\bot SH \\
\end{aligned} \right.\Rightarrow BD\bot \left( SHK \right)\Rightarrow BD\bot HI $, mà $ HI\bot SK $, suy ra $ HI\bot \left( SBD \right)$.
Khi đó, ta có $\text{d}\left( A ,\left( SBD \right) \right)=\text{d}\left( H,\left( SBD \right) \right).\dfrac{AB}{HB}=2HI$.
Trong $\Delta SAB$ đều, ta có $SH=AB\dfrac{\sqrt{3}}{2}=a\sqrt{3}$.
Trong $\Delta ABD$ vuông tại $A$, ta có $\dfrac{1}{A{{M}^{2}}}=\dfrac{1}{A{{B}^{2}}}+\dfrac{1}{A{{D}^{2}}}\Rightarrow AM=\dfrac{2a\sqrt{5}}{5}\Rightarrow HK=\dfrac{1}{2}AM=\dfrac{a\sqrt{5}}{5}$.
Trong $\Delta SHK$ vuông tại $H$, ta có $\dfrac{1}{H{{I}^{2}}}=\dfrac{1}{S{{H}^{2}}}+\dfrac{1}{H{{K}^{2}}}\Rightarrow HI=\dfrac{a\sqrt{3}}{4}$.
Vậy $\text{d}\left( A ,\left( SBD \right) \right)=\dfrac{a\sqrt{3}}{2}$.
Đáp án B.
