Google
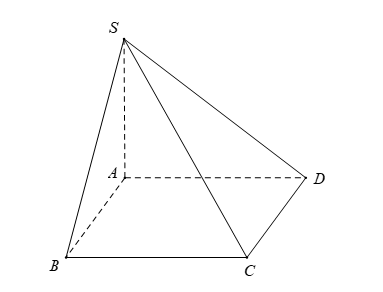
Câu hỏi: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $2a$, $SA\bot \left( ABCD \right)$ và $SA=a$ (tham khảo hình vẽ dưới đây).
Khoảng cách từ điểm $C$ đến mặt phẳng $\left( SBD \right)$ bằng
A. $\dfrac{2\sqrt{2}}{3}a.$
B. $\dfrac{\sqrt{3}}{4}a.$
C. $\dfrac{\sqrt{6}}{3}a.$
D. $\dfrac{\sqrt{2}}{3}a.$
A. $\dfrac{2\sqrt{2}}{3}a.$
B. $\dfrac{\sqrt{3}}{4}a.$
C. $\dfrac{\sqrt{6}}{3}a.$
D. $\dfrac{\sqrt{2}}{3}a.$
Cách 1: Sử dụng kiến thức hình học không gian.
Trong $\left( ABCD \right),$ gọi $O=AC\cap BD$.
Ta có $\left\{ \begin{aligned}
& BD\bot AC \\
& BD\bot SA \\
\end{aligned} \right.\Rightarrow BD\bot \left( SAC \right)\Rightarrow \left( SBD \right)\bot \left( SAC \right) $ mà $ \left( SBD \right)\cap \left( SAC \right)=SO $, do đó từ $ C $ kẻ $ CH\bot SO $ với $ H\in SO $ thì $ CH\bot \left( SBD \right) $. Vậy $ d\left( C,\left( SBD \right) \right)=CH$.
Lại có $\Delta SAO$ ∽ $\Delta CHO$ nên $\dfrac{SA}{CH}=\dfrac{SO}{CO}\Rightarrow CH=\dfrac{SA.CO}{SO}=\dfrac{SA.\dfrac{AC}{2}}{\sqrt{S{{A}^{2}}+A{{O}^{2}}}}=\dfrac{a.\dfrac{2a\sqrt{2}}{2}}{\sqrt{{{a}^{2}}+{{\left( \dfrac{2a\sqrt{2}}{2} \right)}^{2}}}}=\dfrac{\sqrt{6}a}{3}$.
Cách 2: Sử dụng phương pháp toạ độ hoá.
Gắn hệ trục toạ độ $Oxyz$ sao cho $A\equiv O\left( 0;0;0 \right),B\left( 2a;0;0 \right),D\left( 0;2a;0 \right),S\left( 0;0;a \right)$ thì $C\left( 2a;2a;0 \right)$.
Khi đó, phương trình mặt phẳng $\left( SBD \right)$ có dạng $\dfrac{x}{2a}+\dfrac{y}{2a}+\dfrac{z}{a}=1\Leftrightarrow x+y+2z-2a=0$.
Vậy $d\left( C,\left( SBD \right) \right)=\dfrac{\left| 2a+2a-2a \right|}{\sqrt{{{1}^{2}}+{{1}^{2}}+{{2}^{2}}}}=\dfrac{2a}{\sqrt{6}}=\dfrac{\sqrt{6}a}{3}.$
Ta có $\left\{ \begin{aligned}
& BD\bot AC \\
& BD\bot SA \\
\end{aligned} \right.\Rightarrow BD\bot \left( SAC \right)\Rightarrow \left( SBD \right)\bot \left( SAC \right) $ mà $ \left( SBD \right)\cap \left( SAC \right)=SO $, do đó từ $ C $ kẻ $ CH\bot SO $ với $ H\in SO $ thì $ CH\bot \left( SBD \right) $. Vậy $ d\left( C,\left( SBD \right) \right)=CH$.
Lại có $\Delta SAO$ ∽ $\Delta CHO$ nên $\dfrac{SA}{CH}=\dfrac{SO}{CO}\Rightarrow CH=\dfrac{SA.CO}{SO}=\dfrac{SA.\dfrac{AC}{2}}{\sqrt{S{{A}^{2}}+A{{O}^{2}}}}=\dfrac{a.\dfrac{2a\sqrt{2}}{2}}{\sqrt{{{a}^{2}}+{{\left( \dfrac{2a\sqrt{2}}{2} \right)}^{2}}}}=\dfrac{\sqrt{6}a}{3}$.
Cách 2: Sử dụng phương pháp toạ độ hoá.
Khi đó, phương trình mặt phẳng $\left( SBD \right)$ có dạng $\dfrac{x}{2a}+\dfrac{y}{2a}+\dfrac{z}{a}=1\Leftrightarrow x+y+2z-2a=0$.
Vậy $d\left( C,\left( SBD \right) \right)=\dfrac{\left| 2a+2a-2a \right|}{\sqrt{{{1}^{2}}+{{1}^{2}}+{{2}^{2}}}}=\dfrac{2a}{\sqrt{6}}=\dfrac{\sqrt{6}a}{3}.$
Đáp án C.