Google
Câu hỏi: Cho hình chóp $S.ABCD$ có đáy là $ABCD$ là hình vuông, tam giác $SAD$ cân tại $S$ và nằm trong mặt phẳng vuông góc với đáy $ABCD$. Biết $SD=a$, gọi $K$ là trung điểm của $AB$, góc giữa đường thẳng $SK$ với mặt phẳng đáy bằng $60{}^\circ $. Thể tích $V$ của khối chóp $S.ABCD$ bằng
A. $V=\dfrac{4{{a}^{3}}\sqrt{42}}{147}$.
B. $V=\dfrac{2{{a}^{3}}\sqrt{42}}{49}$.
C. $V=\dfrac{4{{a}^{3}}\sqrt{42}}{49}$.
D. $V=\dfrac{2{{a}^{3}}\sqrt{42}}{147}$.
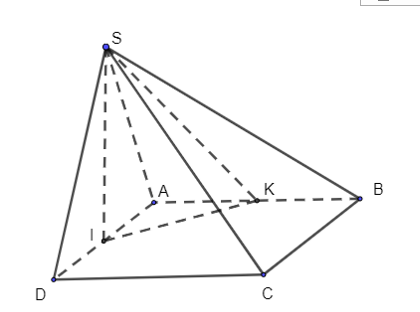Gọi $I$ là trung điểm của $AD$.
Ta có $SI\bot AD$ ( do $\Delta SAD$ cân tại $S$ ) và $\left( SAD \right)\bot \left( ABCD \right)$ nên $SI\bot \left( ABCD \right)$.
Từ $SI\bot \left( ABCD \right)$ nên $\left( SK,\left( ABCD \right) \right)=\left( SK,IK \right)=\widehat{SKI}=60{}^\circ $.
Xét tam giác $SIK$ vuông tại $I$ nên $\tan 60{}^\circ =\dfrac{SI}{IK}\Rightarrow SI=IK.\sqrt{3}$.(1)
Gọi độ dài cạnh hình vuông $ABCD$ là $x$. Khi đó ta có $BD=x\sqrt{2}$.
Xét tam giác $ABD$ có $IK$ là đường trung bình nên $IK=x\dfrac{\sqrt{2}}{2}$.(2)
Từ (1),(2) ta có $SI=x\dfrac{\sqrt{6}}{2}$. (*)
Mặt khác tam giác $SDI$ vuông tại $I$ nên ta có $SI=\sqrt{{{a}^{2}}-\dfrac{{{x}^{2}}}{4}}$. (**)
Từ (*),(**) suy ra $\dfrac{3}{2}{{x}^{2}}={{a}^{2}}-\dfrac{{{x}^{2}}}{4}\Leftrightarrow {{a}^{2}}=\dfrac{7}{4}{{x}^{2}}\Leftrightarrow x=\dfrac{2}{\sqrt{7}}a$.( Vì $a,x>0$ )
Suy ra $SI=\dfrac{\sqrt{6}}{2}.\dfrac{2}{\sqrt{7}}a=\dfrac{\sqrt{6}}{\sqrt{7}}a$.
Vậy thể tích $S.ABCD$ là $V=\dfrac{1}{3}.SI.{{S}_{ABCD}}=\dfrac{1}{3}\dfrac{\sqrt{6}}{\sqrt{7}}a.{{\left( \dfrac{2}{\sqrt{7}} \right)}^{2}}.{{a}^{2}}=\dfrac{4\sqrt{42}{{a}^{3}}}{147}$.
A. $V=\dfrac{4{{a}^{3}}\sqrt{42}}{147}$.
B. $V=\dfrac{2{{a}^{3}}\sqrt{42}}{49}$.
C. $V=\dfrac{4{{a}^{3}}\sqrt{42}}{49}$.
D. $V=\dfrac{2{{a}^{3}}\sqrt{42}}{147}$.
Ta có $SI\bot AD$ ( do $\Delta SAD$ cân tại $S$ ) và $\left( SAD \right)\bot \left( ABCD \right)$ nên $SI\bot \left( ABCD \right)$.
Từ $SI\bot \left( ABCD \right)$ nên $\left( SK,\left( ABCD \right) \right)=\left( SK,IK \right)=\widehat{SKI}=60{}^\circ $.
Xét tam giác $SIK$ vuông tại $I$ nên $\tan 60{}^\circ =\dfrac{SI}{IK}\Rightarrow SI=IK.\sqrt{3}$.(1)
Gọi độ dài cạnh hình vuông $ABCD$ là $x$. Khi đó ta có $BD=x\sqrt{2}$.
Xét tam giác $ABD$ có $IK$ là đường trung bình nên $IK=x\dfrac{\sqrt{2}}{2}$.(2)
Từ (1),(2) ta có $SI=x\dfrac{\sqrt{6}}{2}$. (*)
Mặt khác tam giác $SDI$ vuông tại $I$ nên ta có $SI=\sqrt{{{a}^{2}}-\dfrac{{{x}^{2}}}{4}}$. (**)
Từ (*),(**) suy ra $\dfrac{3}{2}{{x}^{2}}={{a}^{2}}-\dfrac{{{x}^{2}}}{4}\Leftrightarrow {{a}^{2}}=\dfrac{7}{4}{{x}^{2}}\Leftrightarrow x=\dfrac{2}{\sqrt{7}}a$.( Vì $a,x>0$ )
Suy ra $SI=\dfrac{\sqrt{6}}{2}.\dfrac{2}{\sqrt{7}}a=\dfrac{\sqrt{6}}{\sqrt{7}}a$.
Vậy thể tích $S.ABCD$ là $V=\dfrac{1}{3}.SI.{{S}_{ABCD}}=\dfrac{1}{3}\dfrac{\sqrt{6}}{\sqrt{7}}a.{{\left( \dfrac{2}{\sqrt{7}} \right)}^{2}}.{{a}^{2}}=\dfrac{4\sqrt{42}{{a}^{3}}}{147}$.
Đáp án A.