Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân...

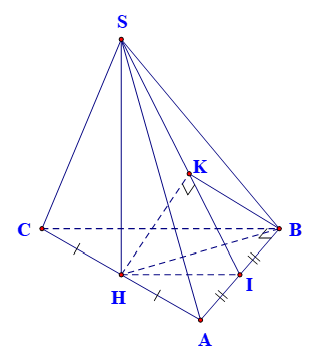Gọi $H$ là trung điểm $AC\Rightarrow SH\bot AC\Rightarrow SH\bot \left( ABC \right)$.
Dễ thấy tam giác $ABC$ vuông cân tại $B$.
Gọi $I$ là trung điểm $AB\Rightarrow HI\bot AB$ suy ra $AB\bot \left( SHI \right)\Rightarrow \left( SAB \right)\bot \left( SHI \right)$.
Vẽ $HK\bot SI$ tại $K$ trong $\left( SHI \right)$.
Khi đó $\left\{ \begin{aligned}
& \left( SHI \right)\bot \left( SAB \right) \\
& \left( SHI \right)\cap \left( SAB \right)=SI \\
& \text{Trong }\left( SHI \right),HK\bot SI \\
\end{aligned} \right.\Rightarrow HK\bot \left( SAB \right)$.
Dễ thấy $HB\bot \left( SAC \right)$ nên $\widehat{\left[ \left( SAC \right);\left( SAB \right) \right]}=\widehat{\left( HK;HB \right)}=\widehat{BHK}$.
Ta có $AC=BC\sqrt{2}=2a\sqrt{2}\Rightarrow BH=\dfrac{AC}{2}=a\sqrt{2}$ ; $HI=\dfrac{1}{2}BC=a$.
$SH=\sqrt{S{{A}^{2}}-A{{H}^{2}}}=\sqrt{3{{a}^{2}}-2{{a}^{2}}}=a\Rightarrow HK=\dfrac{SH.HI}{\sqrt{S{{H}^{2}}+H{{I}^{2}}}}=\dfrac{a.a}{\sqrt{{{a}^{2}}+{{a}^{2}}}}=\dfrac{a\sqrt{2}}{2}$.
Khi đó $\cos \widehat{BHK}=\dfrac{HK}{BH}=\dfrac{1}{2}\Rightarrow \widehat{BHK}=60{}^\circ $.
Vậy $\widehat{\left[ \left( SAC \right);\left( SAB \right) \right]}=60{}^\circ $.