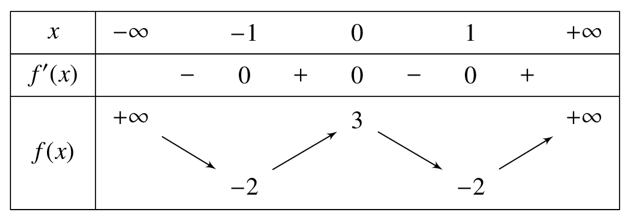
Cho hàm số $y=f(x)$ là hàm số đa thức bậc bốn và có bảng biến...

Ta có: $g(x)={{10}^{\dfrac{-1}{{{x}^{4}}}}}{{\left[ f\left( 2x+1 \right) \right]}^{3}}.$
$\Rightarrow {g}'(x)={{10}^{\dfrac{-1}{{{x}^{4}}}}}\dfrac{4\ln 10}{{{x}^{5}}}{{\left[ f\left( 2x+1 \right) \right]}^{3}}+{{10}^{\dfrac{-1}{{{x}^{4}}}}}.3.2{f}'\left( 2x+1 \right){{\left[ f\left( 2x+1 \right) \right]}^{2}}$
$\Leftrightarrow {g}'(x)={{2.10}^{\dfrac{-1}{{{x}^{4}}}}}{{\left[ f\left( 2x+1 \right) \right]}^{2}}\left( \dfrac{2\ln 10}{{{x}^{5}}}f\left( 2x+1 \right)+3{f}'\left( 2x+1 \right) \right)=0$
$\Leftrightarrow \left[ \begin{aligned}
& {{f}^{2}}\left( 2x+1 \right)=0 \\
& \begin{matrix}
\dfrac{2\ln 10}{{{x}^{5}}}f\left( 2x+1 \right)+3{f}'\left( 2x+1 \right)=0 & \left( * \right) \\
\end{matrix} \\
\end{aligned} \right.$
Do các nghiệm của phương trình ${{f}^{2}}\left( 2x+1 \right)=0$ là các nghiệm bội chẵn nên số điểm cực trị của hàm số $g\left( x \right)$ là số nghiệm bội lẻ của phương trình $\left( * \right)$.
Xét phương trình $\dfrac{2\ln 10}{{{x}^{5}}}f\left( 2x+1 \right)+3{f}'\left( 2x+1 \right)=0$.
Đặt $t=2x+1$ ta được $\dfrac{{{2}^{6}}.\ln 10}{{{\left( t-1 \right)}^{5}}}f(t)+3{f}'(t)=0$.
Từ bảng biến thiên ta thấy được phương trình $f\left( t \right)=0$ có 4 nghiệm ${{t}_{1}}$, ${{t}_{2}}$, ${{t}_{3}}$, ${{t}_{4}}$.
$\Rightarrow f\left( t \right)=a\left( t-{{t}_{1}} \right)\left( t-{{t}_{2}} \right)\left( t-{{t}_{3}} \right)\left( t-{{t}_{4}} \right)$
$\Rightarrow {f}'\left( t \right)=a\left[ \left( t-{{t}_{2}} \right)\left( t-{{t}_{3}} \right)\left( t-{{t}_{4}} \right)+\left( t-{{t}_{1}} \right)\left( t-{{t}_{3}} \right)\left( t-{{t}_{4}} \right)+\left( t-{{t}_{1}} \right)\left( t-{{t}_{2}} \right)\left( t-{{t}_{4}} \right)+\left( t-{{t}_{1}} \right)\left( t-{{t}_{2}} \right)\left( t-{{t}_{3}} \right) \right]$
Do 4 nghiệm ${{t}_{1}}$, ${{t}_{2}}$, ${{t}_{3}}$, ${{t}_{4}}$ không là nghiệm của phương trình $\left( * \right)$ nên:
$\begin{matrix}
\dfrac{{{2}^{6}}.\ln 10}{{{\left( t-1 \right)}^{5}}}f(t)+3{f}'(t)=0\Rightarrow \dfrac{{{2}^{6}}.\ln 10}{{{\left( t-1 \right)}^{5}}}+3\dfrac{{f}'(t)}{f(t)}=0 & \left( ** \right) \\
\end{matrix}$
Thay $f\left( t \right)$ và ${f}'\left( t \right)$ vào $\left( ** \right)$ ta có:
$\dfrac{{{2}^{6}}\ln 10}{{{\left( t-1 \right)}^{5}}}+\dfrac{3}{t-{{t}_{1}}}+\dfrac{3}{t-{{t}_{2}}}+\dfrac{3}{t-{{t}_{3}}}+\dfrac{3}{t-{{t}_{4}}}=0$
Xét hàm số $h\left( t \right)=\dfrac{{{2}^{6}}\ln 10}{{{\left( t-1 \right)}^{5}}}+\dfrac{3}{t-{{t}_{1}}}+\dfrac{3}{t-{{t}_{2}}}+\dfrac{3}{t-{{t}_{3}}}+\dfrac{3}{t-{{t}_{4}}}$ với $t\ne 1,t\ne {{t}_{i}}\left( i=\overline{1,4} \right)$.
$\Rightarrow {h}'\left( t \right)=\dfrac{-{{2}^{6}}.5.\ln 10}{{{\left( t-1 \right)}^{6}}}+\dfrac{-3}{{{\left( t-{{t}_{1}} \right)}^{2}}}+\dfrac{-3}{{{\left( t-{{t}_{2}} \right)}^{2}}}+\dfrac{-3}{{{\left( t-{{t}_{3}} \right)}^{2}}}+\dfrac{-3}{{{\left( t-{{t}_{4}} \right)}^{2}}}<0,{{\forall }^{{}}}t\ne 1,t\ne {{t}_{i}}\left( i=\overline{1,4} \right)$.
Ta có bảng biến thiên của $h\left( t \right)$ :
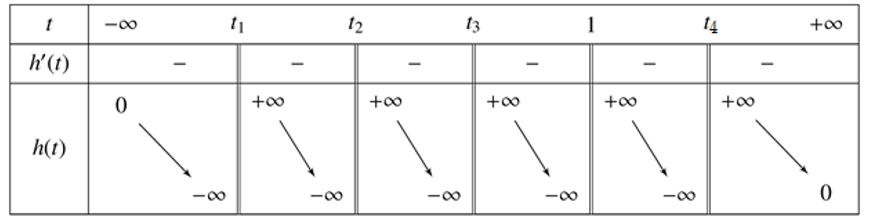Từ bảng biến thiên ta thấy phương trình $h\left( t \right)=0$ luôn có 4 nghiệm đơn phân biệt do đó hàm số $g(x)$ có 4 điểm cực trị.