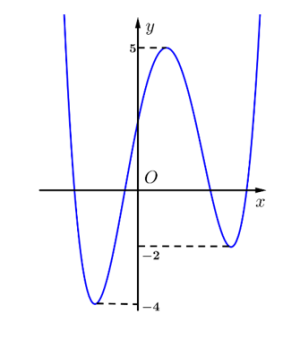
Câu hỏi: Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$ và có đồ thị hàm số $f^{\prime}(x)$ như hình vẽ bên. Có tất cả bao nhiêu giá trị nguyên của tham số $m$ để hàm số $g(x)=f(x)-m x$ có đúng hai điểm cực tiểu?
A. 6 .
B. 7 .
C. 9 .
D. 8 .
A. 6 .
B. 7 .
C. 9 .
D. 8 .
Ta có: $g^{\prime}(x)=f^{\prime}(x)-m$.
Từ đồ thị hàm số $f^{\prime}(x)$ ta thấy hàm số $f^{\prime}(x)$ liên tục trên $\mathbb{R}$ nên hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ do đó hàm số $g(x)=f(x)-m x$ cũng liên tục trên $\mathbb{R}$, từ đó hàm số $g(x)=f(x)-m x$ có đúng hai điểm cực tiểu suy ra hàm số $g(x)=f(x)-m x$ phải có ít nhất 3 điểm cực trị ( 2 điểm cực tiểu và it nhất 1 điểm cực đại). Do đó phương trình $g^{\prime}(x)=0$ hay $f^{\prime}(x)=m$ phải có ít nhất 3 nghiệm phân biệt (không tính nghiệm kép).
Mà số nghiệm của phương trình $f^{\prime}(x)=m$ là số điểm chung của đồ thị hàm số $f^{\prime}(x)$ và đường thẳng $y=m$, từ đồ thị hàm số $f^{\prime}(x)$ suy ra: $-2<m<5$.
Vì $m$ nguyên nên $m \in\{-1 ; 0 ; 1 ; 2 ; 3 ; 4\}$.
Từ đồ thị hàm số $f^{\prime}(x)$ ta thấy hàm số $f^{\prime}(x)$ liên tục trên $\mathbb{R}$ nên hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ do đó hàm số $g(x)=f(x)-m x$ cũng liên tục trên $\mathbb{R}$, từ đó hàm số $g(x)=f(x)-m x$ có đúng hai điểm cực tiểu suy ra hàm số $g(x)=f(x)-m x$ phải có ít nhất 3 điểm cực trị ( 2 điểm cực tiểu và it nhất 1 điểm cực đại). Do đó phương trình $g^{\prime}(x)=0$ hay $f^{\prime}(x)=m$ phải có ít nhất 3 nghiệm phân biệt (không tính nghiệm kép).
Mà số nghiệm của phương trình $f^{\prime}(x)=m$ là số điểm chung của đồ thị hàm số $f^{\prime}(x)$ và đường thẳng $y=m$, từ đồ thị hàm số $f^{\prime}(x)$ suy ra: $-2<m<5$.
Vì $m$ nguyên nên $m \in\{-1 ; 0 ; 1 ; 2 ; 3 ; 4\}$.
Đáp án A.