Google
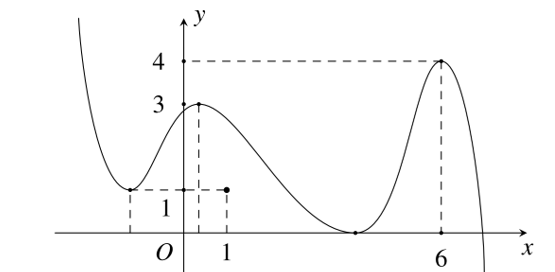
Câu hỏi: Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị hàm số $y={f}'\left( x \right)$ như hình vẽ. Hàm số $g\left( x \right)=f\left( {{x}^{2}} \right)-2x$ có bao nhiêu điểm cực trị?
A. $10$.
B. $5$.
C. $9$.
D. $4$.
B. $5$.
C. $9$.
D. $4$.
Tính đạo hàm: ${g}'\left( x \right)=2x{f}'\left( {{x}^{2}} \right)-2 \left( * \right)$.
Nhận xét: ${g}'\left( 0 \right)=-2\ne 0$ nên $x=0$ không phải là nghiệm của phương trình $\left( * \right)$.
Với $x\ne 0,$ ${g}'\left( x \right)=0\Leftrightarrow 2x{f}'\left( {{x}^{2}} \right)-2=0\Leftrightarrow {f}'\left( {{x}^{2}} \right)=\dfrac{1}{x} \left( ** \right)$.
Đặt $t={{x}^{2}}\Rightarrow \left[ \begin{aligned}
& x=\sqrt{t} \left( x>0 \right) \\
& x=-\sqrt{t} \left( x<0 \right) \\
\end{aligned} \right. $. Phương trình $ \left( ** \right) $ trở thành $ \left[ \begin{aligned}
& {f}'\left( t \right)=\dfrac{1}{\sqrt{t}} \left( 1 \right) \\
& {f}'\left( t \right)=-\dfrac{1}{\sqrt{t}} \left( 2 \right) \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& \left[ \begin{aligned}
& t=a >0 \\
& t=b >0 \\
& t=c >0 \\
& t=d >0 \\
\end{aligned} \right. \\
& t=e >0 \\
\end{aligned} \right.$
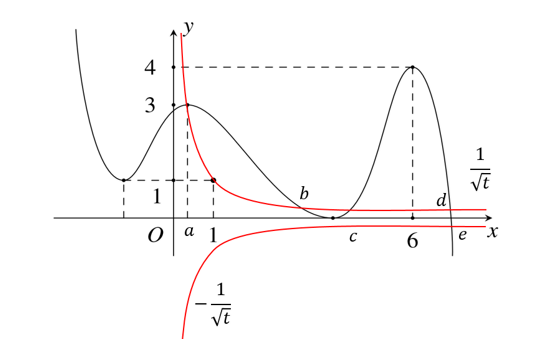Với $t={{x}^{2}}\Rightarrow \left[ \begin{aligned}
& x=\sqrt{a} ; \sqrt{b} ;\sqrt{c} ;\sqrt{d} \left( x\ge 0 \right) \\
& x=-\sqrt{e} \left( x<0 \right) \\
\end{aligned} \right.$
Tất cả 5 nghiệm trên đều là nghiệm bội lẻ nên ${g}'\left( x \right)$ đổi dấu khi qua các nghiệm này. Vậy hàm số $g\left( x \right)$ có tổng cộng 5 điểm cực trị.
Nhận xét: ${g}'\left( 0 \right)=-2\ne 0$ nên $x=0$ không phải là nghiệm của phương trình $\left( * \right)$.
Với $x\ne 0,$ ${g}'\left( x \right)=0\Leftrightarrow 2x{f}'\left( {{x}^{2}} \right)-2=0\Leftrightarrow {f}'\left( {{x}^{2}} \right)=\dfrac{1}{x} \left( ** \right)$.
Đặt $t={{x}^{2}}\Rightarrow \left[ \begin{aligned}
& x=\sqrt{t} \left( x>0 \right) \\
& x=-\sqrt{t} \left( x<0 \right) \\
\end{aligned} \right. $. Phương trình $ \left( ** \right) $ trở thành $ \left[ \begin{aligned}
& {f}'\left( t \right)=\dfrac{1}{\sqrt{t}} \left( 1 \right) \\
& {f}'\left( t \right)=-\dfrac{1}{\sqrt{t}} \left( 2 \right) \\
\end{aligned} \right.\Leftrightarrow \left[ \begin{aligned}
& \left[ \begin{aligned}
& t=a >0 \\
& t=b >0 \\
& t=c >0 \\
& t=d >0 \\
\end{aligned} \right. \\
& t=e >0 \\
\end{aligned} \right.$
& x=\sqrt{a} ; \sqrt{b} ;\sqrt{c} ;\sqrt{d} \left( x\ge 0 \right) \\
& x=-\sqrt{e} \left( x<0 \right) \\
\end{aligned} \right.$
Tất cả 5 nghiệm trên đều là nghiệm bội lẻ nên ${g}'\left( x \right)$ đổi dấu khi qua các nghiệm này. Vậy hàm số $g\left( x \right)$ có tổng cộng 5 điểm cực trị.
Đáp án B.