Câu hỏi: Cho hàm số $f\left( x \right)=\dfrac{2}{5}{{x}^{5}}-\dfrac{m}{2}{{x}^{4}}+\dfrac{4\left( m+3 \right)}{3}{{x}^{3}}-\left( m+7 \right){{x}^{2}}$ với $m$ là tham số. Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $g\left( x \right)=f\left( \left| x \right| \right)$ có đúng một điểm cực đại?
A. $16.$
B. $17.$
C. $12.$
D. $13.$
A. $16.$
B. $17.$
C. $12.$
D. $13.$
Ta có ${f}'\left( x \right)=2{{x}^{4}}-2m{{x}^{3}}+4\left( m+3 \right){{x}^{2}}-2\left( m+7 \right)x=2x\left[ {{x}^{3}}-m{{x}^{2}}+2\left( m+3 \right)x-m-7 \right]$
Ta thấy phương trình ${{x}^{3}}-m{{x}^{2}}+2\left( m+3 \right)x-m-7=0$ có nghiệm là $x=1$
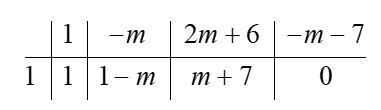
Ta thấy phương trình ${{x}^{3}}-m{{x}^{2}}+2\left( m+3 \right)x-m-7=0$ có nghiệm là $x=1$
Khi đó ta có ${f}'\left( x \right)=0\Leftrightarrow 2x\left( x-1 \right)\left[ {{x}^{2}}+\left( 1-m \right)x+m+7 \right]=0$
Do $\underset{x\to +\infty }{\mathop{\lim }} f\left( x \right)=+\infty $ nên để hàm số $g\left( x \right)=f\left( \left| x \right| \right)$ có đúng một điểm cực đại khi $f\left( x \right)$ có một điểm cực trị dương.
Trường hợp 1: Phương trình ${{x}^{2}}+\left( 1-m \right)x+m+7=0$ có hai nghiệm phân biệt không dương
$\Leftrightarrow \left\{ \begin{matrix}
{{\left( 1-m \right)}^{2}}-4\left( m+7 \right)>0 \\
m-1\le 0 \\
m+7\ge 0 \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
{{m}^{2}}-6m-27>0 \\
m\le 1 \\
m\ge -7 \\
\end{matrix} \right.\Leftrightarrow -7\le m<-3\Rightarrow m\in \left\{ -7;-6;-5;-4 \right\}$.
Trường hợp 2: Phương trình ${{x}^{2}}+\left( 1-m \right)x+m+7=0$ vô nghiệm hoặc có nghiệm kép
$\Leftrightarrow {{\left( 1-m \right)}^{2}}-4\left( m+7 \right)\le 0\Leftrightarrow {{m}^{2}}-6m-27\le 0\Leftrightarrow -3\le m\le 9\Rightarrow m\in \left\{ -3;-2;...;9 \right\}$.
Trường hợp 3: Phương trình ${{x}^{2}}+\left( 1-m \right)x+m+7=0$ có nghiệm $x=1$.
$\Leftrightarrow {{1}^{2}}+\left( 1-m \right)1+m+7=0\Leftrightarrow 9=0$ (Vô lý). Vậy $m\in \left\{ -7;-6;...;8;9 \right\}$.
Do $\underset{x\to +\infty }{\mathop{\lim }} f\left( x \right)=+\infty $ nên để hàm số $g\left( x \right)=f\left( \left| x \right| \right)$ có đúng một điểm cực đại khi $f\left( x \right)$ có một điểm cực trị dương.
Trường hợp 1: Phương trình ${{x}^{2}}+\left( 1-m \right)x+m+7=0$ có hai nghiệm phân biệt không dương
$\Leftrightarrow \left\{ \begin{matrix}
{{\left( 1-m \right)}^{2}}-4\left( m+7 \right)>0 \\
m-1\le 0 \\
m+7\ge 0 \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
{{m}^{2}}-6m-27>0 \\
m\le 1 \\
m\ge -7 \\
\end{matrix} \right.\Leftrightarrow -7\le m<-3\Rightarrow m\in \left\{ -7;-6;-5;-4 \right\}$.
Trường hợp 2: Phương trình ${{x}^{2}}+\left( 1-m \right)x+m+7=0$ vô nghiệm hoặc có nghiệm kép
$\Leftrightarrow {{\left( 1-m \right)}^{2}}-4\left( m+7 \right)\le 0\Leftrightarrow {{m}^{2}}-6m-27\le 0\Leftrightarrow -3\le m\le 9\Rightarrow m\in \left\{ -3;-2;...;9 \right\}$.
Trường hợp 3: Phương trình ${{x}^{2}}+\left( 1-m \right)x+m+7=0$ có nghiệm $x=1$.
$\Leftrightarrow {{1}^{2}}+\left( 1-m \right)1+m+7=0\Leftrightarrow 9=0$ (Vô lý). Vậy $m\in \left\{ -7;-6;...;8;9 \right\}$.
Đáp án B.