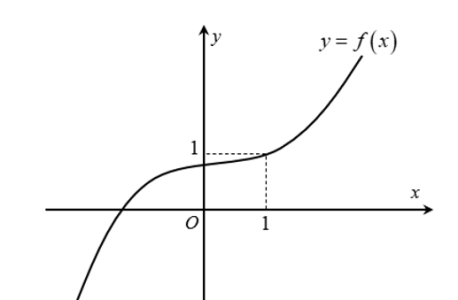
Câu hỏi: Cho hàm số $f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có đồ thị như hình vẽ bên. Có bao nhiêu số thực $m$ để bất phương trình $\left( x-1 \right)\left( {{m}^{3}}f\left( 2x-1 \right)-mf\left( x \right)+f\left( x \right)-1 \right)\ge 0$ nghiệm đúng với mọi $x\in \mathbb{R}$.
A. $2$.
B. $3$.
C. $1$.
D. $0$.
A. $2$.
B. $3$.
C. $1$.
D. $0$.
Để $g\left( x \right)=\left( x-1 \right)\left( {{m}^{3}}f\left( 2x-1 \right)-mf\left( x \right)+f\left( x \right)-1 \right)\ge 0,\forall x$
thì trước tiên ${{m}^{3}}f\left( 2x-1 \right)-mf\left( x \right)+f\left( x \right)-1=0$ phải có nghiệm $x=1$.
$\Leftrightarrow {{m}^{3}}f\left( 1 \right)-mf\left( 1 \right)+f\left( 1 \right)-1=0$ $\Leftrightarrow {{m}^{3}}-m=0\Leftrightarrow m=0;m=\pm 1$.
Với $m=0\Rightarrow g\left( x \right)=\left( x-1 \right)\left( f\left( x \right)-1 \right)\ge 0,\forall x$ thoả mãn.
Với $m=1\Rightarrow g\left( x \right)=\left( x-1 \right)\left( f\left( 2x-1 \right)-1 \right)\ge 0,\forall x$ thoả mãn.
Ta có $\left\{ \begin{aligned}
& \underset{x\to +\infty }{\mathop{\lim }} \left( x-1 \right)=+\infty \\
& \underset{x\to +\infty }{\mathop{\lim }} \left( -f\left( 2x-1 \right)+2f\left( x \right)-1 \right)=\underset{x\to +\infty }{\mathop{\lim }} \left( -8a{{x}^{3}}+2a{{x}^{2}} \right)=\underset{x\to +\infty }{\mathop{\lim }} 6a{{x}^{3}}=-\infty \\
\end{aligned} \right.$
Nên $\underset{x\to +\infty }{\mathop{\lim }} \left[ \left( x-1 \right)\left( -f\left( 2x-1 \right)+2f\left( x \right)-1 \right) \right]=-\infty $
Do đó với $m=-1\Rightarrow g\left( x \right)=\left( x-1 \right)\left( -f\left( 2x-1 \right)+2f\left( x \right)-1 \right)\ge 0,\forall x$ không thoả mãn.
Vậy $m\in \left\{ 0;1 \right\}$.
thì trước tiên ${{m}^{3}}f\left( 2x-1 \right)-mf\left( x \right)+f\left( x \right)-1=0$ phải có nghiệm $x=1$.
$\Leftrightarrow {{m}^{3}}f\left( 1 \right)-mf\left( 1 \right)+f\left( 1 \right)-1=0$ $\Leftrightarrow {{m}^{3}}-m=0\Leftrightarrow m=0;m=\pm 1$.
Với $m=0\Rightarrow g\left( x \right)=\left( x-1 \right)\left( f\left( x \right)-1 \right)\ge 0,\forall x$ thoả mãn.
Với $m=1\Rightarrow g\left( x \right)=\left( x-1 \right)\left( f\left( 2x-1 \right)-1 \right)\ge 0,\forall x$ thoả mãn.
Ta có $\left\{ \begin{aligned}
& \underset{x\to +\infty }{\mathop{\lim }} \left( x-1 \right)=+\infty \\
& \underset{x\to +\infty }{\mathop{\lim }} \left( -f\left( 2x-1 \right)+2f\left( x \right)-1 \right)=\underset{x\to +\infty }{\mathop{\lim }} \left( -8a{{x}^{3}}+2a{{x}^{2}} \right)=\underset{x\to +\infty }{\mathop{\lim }} 6a{{x}^{3}}=-\infty \\
\end{aligned} \right.$
Nên $\underset{x\to +\infty }{\mathop{\lim }} \left[ \left( x-1 \right)\left( -f\left( 2x-1 \right)+2f\left( x \right)-1 \right) \right]=-\infty $
Do đó với $m=-1\Rightarrow g\left( x \right)=\left( x-1 \right)\left( -f\left( 2x-1 \right)+2f\left( x \right)-1 \right)\ge 0,\forall x$ không thoả mãn.
Vậy $m\in \left\{ 0;1 \right\}$.
Đáp án A.