Google
Câu hỏi: Cho hàm số $f\left( x \right)=\dfrac{{{x}^{5}}}{5}-{{x}^{2}}+\left( m-1 \right)x-4029$. Có bao nhiêu giá trị nguyên của $m$ để hàm số $y=\left| f\left( x-1 \right)+2022 \right|$ nghịch biến trên khoảng $\left( -\infty ; 2 \right)$ ?
A. $2005$.
B. $2006$.
C. $2007$.
D. $2008$.
A. $2005$.
B. $2006$.
C. $2007$.
D. $2008$.
Ta có: ${f}'\left( x \right)={{x}^{4}}-2x+m-1$.
Đặt $g\left( x \right)=f\left( x-1 \right)+2022\to {g}'\left( x \right)={f}'\left( x-1 \right)={{\left( x-1 \right)}^{4}}-2\left( x-1 \right)+m-1$.
Điều kiện bài toán $\Leftrightarrow \left[ \begin{aligned}
& \left\{ \begin{aligned}
& {g}'\left( x \right)\le 0, \forall x\in \left( -\infty ; 2 \right) \\
& g\left( 2 \right)\ge 0 \\
\end{aligned} \right. \left( loai \right), v\grave{i} \underset{x\to -\infty }{\mathop{\lim }} g\left( x \right)=-\infty \\
& \left\{ \begin{aligned}
& {g}'\left( x \right)\ge 0, \forall x\in \left( -\infty ; 2 \right) \\
& g\left( 2 \right)\le 0 \\
\end{aligned} \right. \left( 2 \right) \\
\end{aligned} \right.$.
Từ $\left( 2 \right)\Rightarrow \left\{ \begin{aligned}
& m\ge -{{\left( x-1 \right)}^{4}}+2x-1, \forall x<2 \\
& f\left( 1 \right)+2022\le 0 \\
\end{aligned} \right.\Rightarrow \left\{ \begin{aligned}
& m\ge \underset{\left( 2; +\infty \right)}{\mathop{\max h\left( x \right)\approx 2,2}} \\
& m\le \dfrac{10044}{5}\approx 2008,9 \\
\end{aligned} \right.$.
Vì hàm $h\left( x \right)=-{{\left( x-1 \right)}^{4}}+2x-1\to {h}'\left( x \right)=-4{{\left( x-1 \right)}^{3}}+2$, ${h}'\left( x \right)=0\Rightarrow x=\sqrt[3]{\dfrac{1}{2}}+1\approx 1,8$.
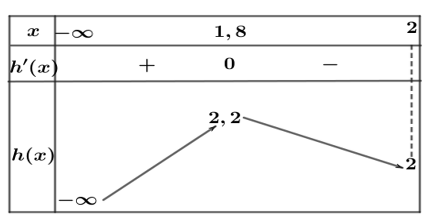Kết hợp $m\in \mathbb{Z}\Rightarrow m\in \left\{ 3; 4;.....; 2008 \right\}\to $ có 2006 giá trị nguyên.
Đặt $g\left( x \right)=f\left( x-1 \right)+2022\to {g}'\left( x \right)={f}'\left( x-1 \right)={{\left( x-1 \right)}^{4}}-2\left( x-1 \right)+m-1$.
Điều kiện bài toán $\Leftrightarrow \left[ \begin{aligned}
& \left\{ \begin{aligned}
& {g}'\left( x \right)\le 0, \forall x\in \left( -\infty ; 2 \right) \\
& g\left( 2 \right)\ge 0 \\
\end{aligned} \right. \left( loai \right), v\grave{i} \underset{x\to -\infty }{\mathop{\lim }} g\left( x \right)=-\infty \\
& \left\{ \begin{aligned}
& {g}'\left( x \right)\ge 0, \forall x\in \left( -\infty ; 2 \right) \\
& g\left( 2 \right)\le 0 \\
\end{aligned} \right. \left( 2 \right) \\
\end{aligned} \right.$.
Từ $\left( 2 \right)\Rightarrow \left\{ \begin{aligned}
& m\ge -{{\left( x-1 \right)}^{4}}+2x-1, \forall x<2 \\
& f\left( 1 \right)+2022\le 0 \\
\end{aligned} \right.\Rightarrow \left\{ \begin{aligned}
& m\ge \underset{\left( 2; +\infty \right)}{\mathop{\max h\left( x \right)\approx 2,2}} \\
& m\le \dfrac{10044}{5}\approx 2008,9 \\
\end{aligned} \right.$.
Vì hàm $h\left( x \right)=-{{\left( x-1 \right)}^{4}}+2x-1\to {h}'\left( x \right)=-4{{\left( x-1 \right)}^{3}}+2$, ${h}'\left( x \right)=0\Rightarrow x=\sqrt[3]{\dfrac{1}{2}}+1\approx 1,8$.
Đáp án B.
