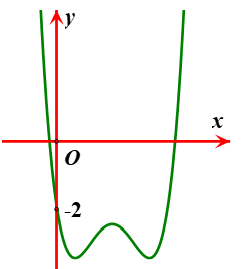
Cho hàm số bậc bốn $y=f\left( x \right)$ có đồ thị là đường cong...

Ta có: $\sqrt{{{x}^{2}}+4}>\sqrt{{{x}^{2}}}=\left| x \right|$
$\Rightarrow \left\{ \begin{aligned}
& \sqrt{{{x}^{2}}+4}+x>\left| x \right|+x\ge 0 \\
& \sqrt{{{x}^{2}}+4}-x>\left| x \right|-x\ge 0 \\
\end{aligned} \right.$
Khi đó, phương trình: $f\left[ g\left( x \right)f\left( x \right) \right]+2=0$
$\Leftrightarrow f\left[ g\left( x \right)f\left( x \right) \right]=-2$
$\Leftrightarrow \left[ \begin{aligned}
& g\left( x \right).f\left( x \right)=0 \\
& g\left( x \right).f\left( x \right)=a\in \left( 0;1 \right) \\
& g\left( x \right).f\left( x \right)=b\in \left( 2;3 \right) \\
& g\left( x \right).f\left( x \right)=c\in \left( 3;4 \right) \\
\end{aligned} \right.$
$\Leftrightarrow \left[ \begin{aligned}
& f\left( x \right)=0\text{ }\left( 1 \right)\text{ }\left( dog\left( x \right)=x+\sqrt{{{x}^{2}}+4}>0,\forall x\in \mathbb{R} \right) \\
& f\left( x \right)=\dfrac{1}{4}a\left( \sqrt{{{x}^{2}}+4}-x \right)\text{ }\left( 2 \right) \\
& f\left( x \right)=\dfrac{1}{4}b\left( \sqrt{{{x}^{2}}+4}-x \right)\text{ }\left( 3 \right) \\
& f\left( x \right)=\dfrac{1}{4}c\left( \sqrt{{{x}^{2}}+4}-x \right)\text{ }\left( 4 \right) \\
\end{aligned} \right.$
Dễ thấy phương trình $f\left( x \right)=0$ có 2 nghiệm phân biệt
Xét hàm số $h\left( x \right)=\dfrac{1}{4}t\left( \sqrt{{{x}^{2}}+4}-x \right),x\in \mathbb{R}\left( t>0 \right)$
${h}'\left( x \right)=\dfrac{1}{4}t\dfrac{x-\sqrt{{{x}^{2}}+4}}{\sqrt{{{x}^{2}}+4}}<0,x\in \mathbb{R}$
$\underset{x\to -\infty }{\mathop{\lim }} h\left( x \right)=+\infty ,\underset{x\to +\infty }{\mathop{\lim }} h\left( x \right)=\underset{x\to +\infty }{\mathop{\lim }} \dfrac{t}{\sqrt{{{x}^{2}}+4}+x}=0$
Từ đồ thị ta thấy các phương trình $\left( 2 \right),\left( 3 \right),\left( 4 \right)$ mỗi phương trình có 2 nghiệm phân biệt
Vậy phương trình đã cho có 8 nghiệm phân biệt.