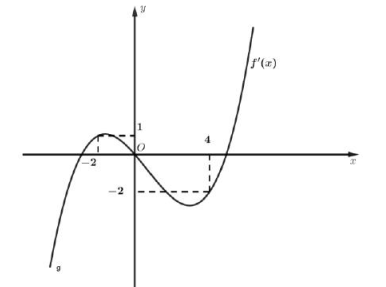
Câu hỏi: Cho hàm số bậc bốn $y=f\left( x \right)$ có đồ thị hàm số $y={f}'\left( x \right)$ như hình vẽ bên. Hàm số $g\left( x \right)=4f\left( {{x}^{2}}-4 \right)+{{x}^{4}}-8{{x}^{2}}$ có bao nhiêu điểm cực tiểu?
A. $3\cdot $
B. $5\cdot $
C. $4\cdot $
D. $7\cdot $
A. $3\cdot $
B. $5\cdot $
C. $4\cdot $
D. $7\cdot $
Ta có ${g}'\left( x \right)=8x.{f}'\left( {{x}^{2}}-4 \right)+4{{x}^{3}}-16x=8x\left( {f}'\left( {{x}^{2}}-4 \right)+\dfrac{{{x}^{2}}-4}{2} \right)$.
Xét ${f}'\left( x \right)+\dfrac{x}{2}=0\Leftrightarrow {f}'\left( x \right)=-\dfrac{x}{2}\Leftrightarrow \left[ \begin{aligned}
& x=-2 \\
& x=0 \\
& x=4 \\
\end{aligned} \right.$.
Suy ra ${f}'\left( x \right)+\dfrac{x}{2}$ là đa thức bậc 3 có các nghiệm $x=-2,x=0,x=4$ nên có dạng
Ta thấy ${g}'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=\pm \sqrt{2} \\
& x=\pm 2\sqrt{2} \\
& x=0 \\
\end{aligned} \right. $ và $ {g}'\left( x \right) $ đổi dấu từ âm sang dương khi đi qua các điểm $ x=-2\sqrt{2},x=-\sqrt{2},x=\sqrt{2},x=2\sqrt{2} $ nên hàm số $ g\left( x \right)$ đã cho có 4 điểm cực tiểu.
Xét ${f}'\left( x \right)+\dfrac{x}{2}=0\Leftrightarrow {f}'\left( x \right)=-\dfrac{x}{2}\Leftrightarrow \left[ \begin{aligned}
& x=-2 \\
& x=0 \\
& x=4 \\
\end{aligned} \right.$.
Suy ra ${f}'\left( x \right)+\dfrac{x}{2}$ là đa thức bậc 3 có các nghiệm $x=-2,x=0,x=4$ nên có dạng
${f}'\left( x \right)+\dfrac{x}{2}=ax\left( x+2 \right)\left( x-4 \right),\left( a>0,\underset{x\to +\infty }{\mathop{\lim }} {f}'\left( x \right)=+\infty \right)$
Do đó: ${g}'\left( x \right)=8ax\left( {{x}^{2}}-4+2 \right)\left( {{x}^{2}}-4 \right)\left( {{x}^{2}}-4-4 \right)=8ax\left( {{x}^{2}}-2 \right)\left( {{x}^{2}}-4 \right)\left( {{x}^{2}}-8 \right)$.Ta thấy ${g}'\left( x \right)=0\Leftrightarrow \left[ \begin{aligned}
& x=\pm \sqrt{2} \\
& x=\pm 2\sqrt{2} \\
& x=0 \\
\end{aligned} \right. $ và $ {g}'\left( x \right) $ đổi dấu từ âm sang dương khi đi qua các điểm $ x=-2\sqrt{2},x=-\sqrt{2},x=\sqrt{2},x=2\sqrt{2} $ nên hàm số $ g\left( x \right)$ đã cho có 4 điểm cực tiểu.
Đáp án C.