Google
Câu hỏi: Cho các số phức $z,w,u$ thỏa mãn $\left| z-4+2i \right|=\left| 2z+\overline{z} \right|$, $\dfrac{w-8-10i}{w-6-10i}$ là số thuần ảo và $\left| u+1-2i \right|=\left| u-2+i \right|$. Giá trị nhỏ nhất của $P=\left| u-z \right|+\left| \overline{u}-\overline{w} \right|$ thuộc khoảng nào sau đây?
A. $\left( 0;5 \right]$
B. $\left( 5;8 \right)$.
C. $\left[ 8;10 \right)$.
D. $\left[ 10;+\infty \right)$.
A. $\left( 0;5 \right]$
B. $\left( 5;8 \right)$.
C. $\left[ 8;10 \right)$.
D. $\left[ 10;+\infty \right)$.
Đầu tiên ta gọi $A,{{N}_{1}},M$ lần lượt là các điểm biểu diễn số phức $z,w,u$ trên mặt phẳng tọa độ $Oxy$.
Khi đó ta có:$\left\{ \begin{aligned}
& A\left( a;b \right):\left| z-4+2i \right|=\left| 2z+\overline{z} \right| \\
& M\left( c;d \right):\left| u+1-2i \right|=\left| u-2+i \right| \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& A\in \left( P \right):y=2{{x}^{2}}+2x-5 \\
& M\in \left( d \right):y=x \\
\end{aligned} \right.$
Đặt $w=x+yi\left( x,y\in \mathbb{R} \right)$, khi đó $e=\dfrac{w-8-10i}{w-6-10i}=k{{i}^{{}}}\left( k\in \mathbb{R} \right)\Leftrightarrow \left( w-8-10i \right)\overline{\left( w-6-10i \right)}=m{{i}^{{}}}\left( m\in \mathbb{R} \right)$
$\Rightarrow \left( w-8-10i \right)\left( \overline{w}-6+10i \right)={{\left| w \right|}^{2}}+\left( -6+10i \right)w-\left( 8+10i \right)\overline{w}+148-20i$ (2)
Thế $w=x+yi\left( x,y\in \mathbb{R} \right)$ vào (2) kết hợp biến đổi đại số, ta được $\operatorname{Re}\left( e \right)={{x}^{2}}-14x+{{y}^{2}}-20y+148=0$, suy ra $N\in \left( C \right):{{\left( x-7 \right)}^{2}}+{{\left( y-10 \right)}^{2}}=1$, tức ${{N}_{1}}$ thuộc đường tròn tâm ${{I}_{1}}\left( 7;10 \right)$, bán kính $R=1$.
Khi đó ta luôn có: $P=\left| u-z \right|+\left| \overline{u-w} \right|=\left| u-z \right|+\left| u-w \right|=MA+M{{N}_{1}}\ge MA+M{{I}_{1}}-1$
Gọi ${{I}_{2}}$ là điểm đối xứng với ${{I}_{1}}\left( 7;10 \right)$ qua $\left( d \right)$, khi đó ta suy ra ${{I}_{2}}\left( 10;7 \right)$ tức ${{N}_{2}}\in \left( {{I}_{2}};1 \right)$.
Khi đó ta có hình vẽ như sau:
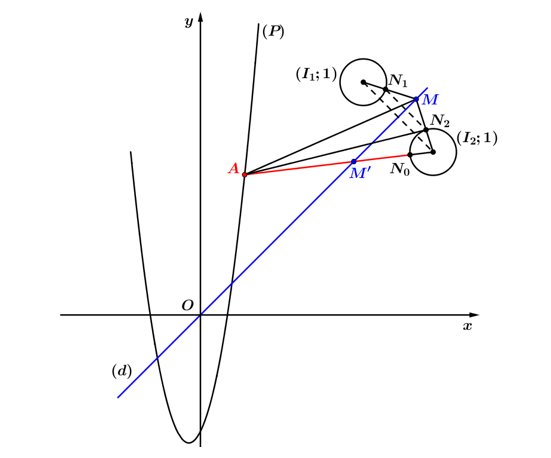Từ hình vẽ, ta dễ dàng suy ra: $P=MA+M{{I}_{1}}-1=MA+M{{I}_{2}}-1=MA+M{{N}_{2}}$
Mặt khác theo bất đẳng thức đường gấp khúc ta luôn có: $MA+M{{N}_{2}}\ge A{{N}_{2}}$ nên $P\ge A{{N}_{2}}=A{{I}_{2}}-1$ khi ${{N}_{2}}\equiv {{N}_{0}}$ tức ${{P}_{\min }}$ khi và chỉ khi $A{{I}_{2}}$ min. Lúc này ta quy về bài toán đơn giản hơn như sau:
“Cho $A\left( a;b \right)\in \left( P \right):y=2{{x}^{2}}+2x-5$ và ${{I}_{2}}\left( 10;7 \right)$, khi ấy tìm giá trị nhỏ nhất của đoạn thẳng $A{{I}_{2}}$ ”.
Lúc này ta có: $A{{I}_{2}}=\sqrt{{{\left( a-10 \right)}^{2}}+{{\left( 2{{a}^{2}}+2a-5-7 \right)}^{2}}}=\sqrt{{{\left( a-10 \right)}^{2}}+4{{\left( {{a}^{2}}+a-6 \right)}^{2}}}$ (Cái hàm mệt mỏi nha).
Chạy TABLE ta suy ra $A{{I}_{2}}\ge \sqrt{63.85}-1\in \left( 5;8 \right)$.
Khi đó ta có:$\left\{ \begin{aligned}
& A\left( a;b \right):\left| z-4+2i \right|=\left| 2z+\overline{z} \right| \\
& M\left( c;d \right):\left| u+1-2i \right|=\left| u-2+i \right| \\
\end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned}
& A\in \left( P \right):y=2{{x}^{2}}+2x-5 \\
& M\in \left( d \right):y=x \\
\end{aligned} \right.$
Đặt $w=x+yi\left( x,y\in \mathbb{R} \right)$, khi đó $e=\dfrac{w-8-10i}{w-6-10i}=k{{i}^{{}}}\left( k\in \mathbb{R} \right)\Leftrightarrow \left( w-8-10i \right)\overline{\left( w-6-10i \right)}=m{{i}^{{}}}\left( m\in \mathbb{R} \right)$
$\Rightarrow \left( w-8-10i \right)\left( \overline{w}-6+10i \right)={{\left| w \right|}^{2}}+\left( -6+10i \right)w-\left( 8+10i \right)\overline{w}+148-20i$ (2)
Thế $w=x+yi\left( x,y\in \mathbb{R} \right)$ vào (2) kết hợp biến đổi đại số, ta được $\operatorname{Re}\left( e \right)={{x}^{2}}-14x+{{y}^{2}}-20y+148=0$, suy ra $N\in \left( C \right):{{\left( x-7 \right)}^{2}}+{{\left( y-10 \right)}^{2}}=1$, tức ${{N}_{1}}$ thuộc đường tròn tâm ${{I}_{1}}\left( 7;10 \right)$, bán kính $R=1$.
Khi đó ta luôn có: $P=\left| u-z \right|+\left| \overline{u-w} \right|=\left| u-z \right|+\left| u-w \right|=MA+M{{N}_{1}}\ge MA+M{{I}_{1}}-1$
Gọi ${{I}_{2}}$ là điểm đối xứng với ${{I}_{1}}\left( 7;10 \right)$ qua $\left( d \right)$, khi đó ta suy ra ${{I}_{2}}\left( 10;7 \right)$ tức ${{N}_{2}}\in \left( {{I}_{2}};1 \right)$.
Khi đó ta có hình vẽ như sau:
Mặt khác theo bất đẳng thức đường gấp khúc ta luôn có: $MA+M{{N}_{2}}\ge A{{N}_{2}}$ nên $P\ge A{{N}_{2}}=A{{I}_{2}}-1$ khi ${{N}_{2}}\equiv {{N}_{0}}$ tức ${{P}_{\min }}$ khi và chỉ khi $A{{I}_{2}}$ min. Lúc này ta quy về bài toán đơn giản hơn như sau:
“Cho $A\left( a;b \right)\in \left( P \right):y=2{{x}^{2}}+2x-5$ và ${{I}_{2}}\left( 10;7 \right)$, khi ấy tìm giá trị nhỏ nhất của đoạn thẳng $A{{I}_{2}}$ ”.
Lúc này ta có: $A{{I}_{2}}=\sqrt{{{\left( a-10 \right)}^{2}}+{{\left( 2{{a}^{2}}+2a-5-7 \right)}^{2}}}=\sqrt{{{\left( a-10 \right)}^{2}}+4{{\left( {{a}^{2}}+a-6 \right)}^{2}}}$ (Cái hàm mệt mỏi nha).
Chạy TABLE ta suy ra $A{{I}_{2}}\ge \sqrt{63.85}-1\in \left( 5;8 \right)$.
Đáp án B.
