Câu hỏi: Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh bên SA vuông góc với đáy và SC tạo với (SAD) góc 30o. Gọi G là trọng tâm tam giác SAB. Tính khoảng cách từ G đến mặt phẳng (SCD).
Lời giải chi tiết
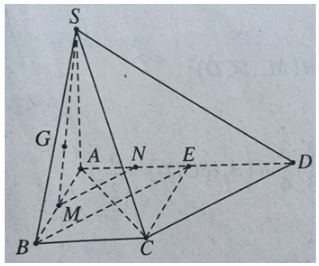
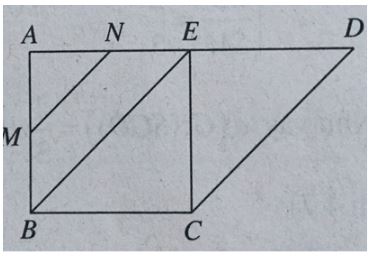
+ Xác định góc của SC với (SAD).
Hạ CE ⊥ AD, ta có E là trung điểm AD và CE ⊥ (SAD) nên ∠(CSE) = 30o.
∠(CSE) cũng chính là góc giữa SC và mp(SAD).
Trong ΔCSE, ta có:
SE = CE. Tan60o = a√3 ⇒ SA = √(SE2- AE2 ) = √(3a2 - a2 ) = a√2.
Nhận xét
Gọi M, N lần lượt là trung điểm của AB và AE.
Ta có MN // BE nên MN // CD. Như vậy MN // (SCD). Ta suy ra
d(M,(SCD)) = d(N,(SCD)).
Mà DN/DA = 3/4 nên d(N,(SCD)) = 3/4 d(A,(SCD))
+ Xác định khoảng cách từ A đến (SCD).
Vì vậy tam giác ACD vuông cân tại C nên CD vuông góc với AC.
CD ⊥ AC & CD ⊥ SA ⇒ CD ⊥ (SAC) ⇒ (SCD) ⊥ (SAC).
Hạ AH ⊥ SC, ta có AH ⊥ (SCD).
Trong tam giác SAC, ta có:
$\frac{1}{A H^{2}}=\frac{1}{A S^{2}}+\frac{1}{A C^{2}}=\frac{1}{2 a^{2}}+\frac{1}{2 a^{2}}=\frac{1}{a^{2}} \Rightarrow \mathrm{AH}=\mathrm{a}$
Ta có: $\left\{\begin{array}{c}S \in(S C D) \\ \frac{S G}{S M}=\frac{2}{3} \quad \text { nên } \mathrm{d}(\mathrm{G},(\mathrm{SCD}))=\frac{2}{3} \mathrm{~d}(\mathrm{M},(\mathrm{SCD}))\end{array}\right.$
Như vậy $\mathrm{d}(\mathrm{G},(\mathrm{SCD}))=\frac{2}{3} \mathrm{~d}(\mathrm{~N},(\mathrm{SCD}))=\frac{2}{3} \cdot \frac{3}{4} \mathrm{~d}(\mathrm{~A},(\mathrm{SCD}))=\frac{a}{2} .$
+ Xác định góc của SC với (SAD).
Hạ CE ⊥ AD, ta có E là trung điểm AD và CE ⊥ (SAD) nên ∠(CSE) = 30o.
∠(CSE) cũng chính là góc giữa SC và mp(SAD).
Trong ΔCSE, ta có:
SE = CE. Tan60o = a√3 ⇒ SA = √(SE2- AE2 ) = √(3a2 - a2 ) = a√2.
Nhận xét
Gọi M, N lần lượt là trung điểm của AB và AE.
Ta có MN // BE nên MN // CD. Như vậy MN // (SCD). Ta suy ra
d(M,(SCD)) = d(N,(SCD)).
Mà DN/DA = 3/4 nên d(N,(SCD)) = 3/4 d(A,(SCD))
+ Xác định khoảng cách từ A đến (SCD).
Vì vậy tam giác ACD vuông cân tại C nên CD vuông góc với AC.
CD ⊥ AC & CD ⊥ SA ⇒ CD ⊥ (SAC) ⇒ (SCD) ⊥ (SAC).
Hạ AH ⊥ SC, ta có AH ⊥ (SCD).
Trong tam giác SAC, ta có:
$\frac{1}{A H^{2}}=\frac{1}{A S^{2}}+\frac{1}{A C^{2}}=\frac{1}{2 a^{2}}+\frac{1}{2 a^{2}}=\frac{1}{a^{2}} \Rightarrow \mathrm{AH}=\mathrm{a}$
Ta có: $\left\{\begin{array}{c}S \in(S C D) \\ \frac{S G}{S M}=\frac{2}{3} \quad \text { nên } \mathrm{d}(\mathrm{G},(\mathrm{SCD}))=\frac{2}{3} \mathrm{~d}(\mathrm{M},(\mathrm{SCD}))\end{array}\right.$
Như vậy $\mathrm{d}(\mathrm{G},(\mathrm{SCD}))=\frac{2}{3} \mathrm{~d}(\mathrm{~N},(\mathrm{SCD}))=\frac{2}{3} \cdot \frac{3}{4} \mathrm{~d}(\mathrm{~A},(\mathrm{SCD}))=\frac{a}{2} .$