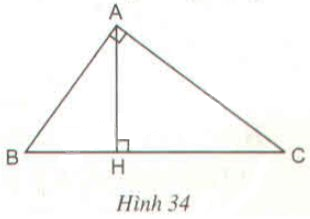
Câu hỏi: Cho tam giác \(ABC\) (\(\widehat A = 90^\circ \)) có đường cao \(AH\) (h.34)
Chứng minh rằng \(A{H^2} = BH.CH\)
Chứng minh rằng \(A{H^2} = BH.CH\)
Phương pháp giải
Sử dụng:
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng. Từ đó suy ra hệ thức về cạnh.
- Hai góc cùng phụ với một góc thứ ba thì bằng nhau.
Lời giải chi tiết
Xét tam giác \(ABC\) vuông tại \(A\) nên \(\widehat {CBA} + \widehat {ACB} = 90^\circ \)
Xét tam giác \(AHC\) vuông tại \(H\) nên \(\widehat {HAC} + \widehat {ACH} = 90^\circ \)
Suy ra \(\widehat {HBA} = \widehat {HAC}\) (hai góc cùng phụ với \(\widehat {ACB}\))
Xét hai tam giác vuông \(HBA\) và \(HAC\) có:
\(\widehat {BHA} = \widehat {AHC} = 90^\circ \)
\(\widehat {HBA} = \widehat {HAC}\) (chứng minh trên)
\( \Rightarrow ∆ HBA \backsim ∆ HAC\) (g.g)
\( \Rightarrow\displaystyle {{HA} \over {HB}} = {{HC} \over {HA}}\)
\( \Rightarrow A{H^2} = HB.HC\) (đpcm).
Sử dụng:
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng. Từ đó suy ra hệ thức về cạnh.
- Hai góc cùng phụ với một góc thứ ba thì bằng nhau.
Lời giải chi tiết
Xét tam giác \(ABC\) vuông tại \(A\) nên \(\widehat {CBA} + \widehat {ACB} = 90^\circ \)
Xét tam giác \(AHC\) vuông tại \(H\) nên \(\widehat {HAC} + \widehat {ACH} = 90^\circ \)
Suy ra \(\widehat {HBA} = \widehat {HAC}\) (hai góc cùng phụ với \(\widehat {ACB}\))
Xét hai tam giác vuông \(HBA\) và \(HAC\) có:
\(\widehat {BHA} = \widehat {AHC} = 90^\circ \)
\(\widehat {HBA} = \widehat {HAC}\) (chứng minh trên)
\( \Rightarrow ∆ HBA \backsim ∆ HAC\) (g.g)
\( \Rightarrow\displaystyle {{HA} \over {HB}} = {{HC} \over {HA}}\)
\( \Rightarrow A{H^2} = HB.HC\) (đpcm).