Câu hỏi: Cho hai tia Ax và By vuông góc với nhau nhận AB làm đoạn vuông góc chung. Gọi M và N là hai điểm di động lần lượt trên Ax và By sao cho AM + BN = MN.
Đặt AB = 2a, gọi O là trung điểm của AB và H là hình chiếu vuông góc điểm O trên đường thẳng MN
a) Chứng minh rằng OH = a, HM = AN, HN = BN.
b) Gọi Bx' là tia song song và cùng chiều với tia Ax và K là hình chiếu vuông góc của H trên mặt phẳng (Bx'; By). Chứng minh BK là phân giác của góc ∠x'By.
c) Chứng minh điểm H nằm trên một đường tròn cố định.
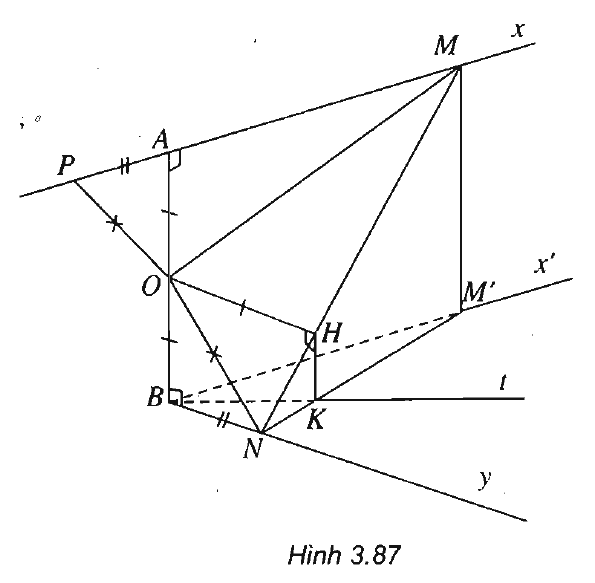
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
Khi đó \(\dfrac{{KM'}}{{KN}} = \dfrac{{HM}}{{HN}} = \dfrac{{AM}}{{BN}} = \dfrac{{BM'}}{{BN}}\)
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK).
Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β).
Trong mặt phẳng (β) ta có OH = a.
Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)
Đặt AB = 2a, gọi O là trung điểm của AB và H là hình chiếu vuông góc điểm O trên đường thẳng MN
a) Chứng minh rằng OH = a, HM = AN, HN = BN.
b) Gọi Bx' là tia song song và cùng chiều với tia Ax và K là hình chiếu vuông góc của H trên mặt phẳng (Bx'; By). Chứng minh BK là phân giác của góc ∠x'By.
c) Chứng minh điểm H nằm trên một đường tròn cố định.
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
Khi đó \(\dfrac{{KM'}}{{KN}} = \dfrac{{HM}}{{HN}} = \dfrac{{AM}}{{BN}} = \dfrac{{BM'}}{{BN}}\)
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK).
Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β).
Trong mặt phẳng (β) ta có OH = a.
Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)