Google
Câu hỏi: Trong không gian $Oxyz$, cho hai điểm $A\left( 1;1;-3 \right)$ và $B\left( -2;3;1 \right)$. Xét hai điểm $M,N$ thay đổi thuộc mặt phẳng $\left( Oxz \right)$ sao cho $MN=2$. Giá trị nhỏ nhất của $AM+BN$ bằng.
A. $5$.
B. $6$.
C. $4$.
D. $7$.
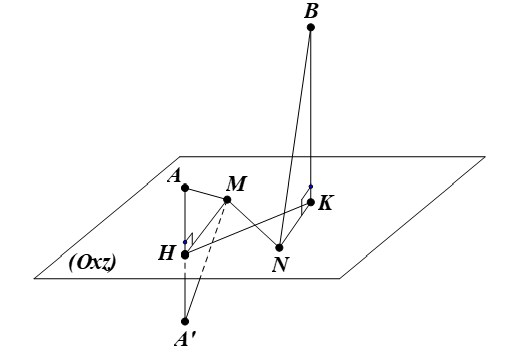Ta có $H\left( 1;0;-3 \right)$, $K\left( -2;0;1 \right)$ lần lượt là hình chiếu vuông góc của $A\left( 1;1;-3 \right)$ và $B\left( -2;3;1 \right)$ xuống mặt phẳng $\left( Oxz \right)$.
Nhận xét: ${A}$, ${B}$ nằm về cùng một phía với mặt phẳng $\left( Oxz \right)$.
Gọi ${A}'$ đối xứng với $A$ qua $\left( Oxz \right)$, suy ra $H$ là trung điểm đoạn $A{A}'$ nên $AM={A}'M$.
Mà ${A}'H=AH=1;BK=3;HK=5$.
Do đó $AM+BN={A}'M+BN=\sqrt{H{{{{A}'}}^{2}}+H{{M}^{2}}}+\sqrt{B{{K}^{2}}+K{{N}^{2}}}$
$\ge \sqrt{{{\left( H{A}'+BK \right)}^{2}}+{{\left( HM+KN \right)}^{2}}}=\sqrt{16+{{\left( HM+KN \right)}^{2}}}$
Lại có $HM+MN+NK\ge HK\Rightarrow HM+NK\ge HK-MN=5-2=3$
Dấu “=” xảy ra khi và chỉ khi $H,M,N,K$ thẳng hàng và theo thứ tự đó.
Suy ra $AM+BN\ge \sqrt{16+{{\left( HM+KN \right)}^{2}}}\ge \sqrt{16+{{\left( 3 \right)}^{2}}}=5$.
Vậy giá trị nhỏ nhất của $AM+BN$ bằng $5$.
A. $5$.
B. $6$.
C. $4$.
D. $7$.
Nhận xét: ${A}$, ${B}$ nằm về cùng một phía với mặt phẳng $\left( Oxz \right)$.
Gọi ${A}'$ đối xứng với $A$ qua $\left( Oxz \right)$, suy ra $H$ là trung điểm đoạn $A{A}'$ nên $AM={A}'M$.
Mà ${A}'H=AH=1;BK=3;HK=5$.
Do đó $AM+BN={A}'M+BN=\sqrt{H{{{{A}'}}^{2}}+H{{M}^{2}}}+\sqrt{B{{K}^{2}}+K{{N}^{2}}}$
$\ge \sqrt{{{\left( H{A}'+BK \right)}^{2}}+{{\left( HM+KN \right)}^{2}}}=\sqrt{16+{{\left( HM+KN \right)}^{2}}}$
Lại có $HM+MN+NK\ge HK\Rightarrow HM+NK\ge HK-MN=5-2=3$
Dấu “=” xảy ra khi và chỉ khi $H,M,N,K$ thẳng hàng và theo thứ tự đó.
Suy ra $AM+BN\ge \sqrt{16+{{\left( HM+KN \right)}^{2}}}\ge \sqrt{16+{{\left( 3 \right)}^{2}}}=5$.
Vậy giá trị nhỏ nhất của $AM+BN$ bằng $5$.
Đáp án A.
