Câu hỏi: Cho tam giác \(ABC\) cân tại \(A\), nội tiếp đường tròn (O). Đường cao \(AH\) cắt đường tròn ở \(D\).
a) Vì sao \(AD\) là đường kính của đường tròn (O)?
b) Tính số đo góc \(ACD\).
c) Cho \(BC = 24cm\), \(AC = 20cm\). Tính đường cao \(AH\) và bán kính đường tròn (O).
a) Vì sao \(AD\) là đường kính của đường tròn (O)?
b) Tính số đo góc \(ACD\).
c) Cho \(BC = 24cm\), \(AC = 20cm\). Tính đường cao \(AH\) và bán kính đường tròn (O).
Phương pháp giải
+ Đường tròn là tập hợp các điểm cách điểm O cố định một khoảng bằng R không đổi (\(R>0\)), O gọi là tâm và R là bán kính.
+ Xét tam giác ABC vuông tại A, có đường cao AH:
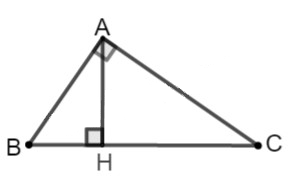
- Áp dụng định lí Pytago: \(B{C^2} = A{B^2} + A{C^2}\)
- Hệ thức lượng trong tam giác vuông: \(A{C^2} = AH.BC\)
Lời giải chi tiết
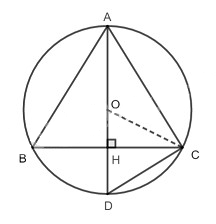
a) Tam giác \(ABC\) cân tại \(A\) nên \(AH\) là đường cao đồng thời cũng là đường trung trực của \(BC\).
Vì \(O\) là tâm của đường tròn ngoại tiếp tam giác \(ABC\) nên \(O\) nằm trên đường trung trực của \(BC\) hay \(O\) thuộc \(AD\).
Suy ra \(AD\) là đường kính của (O).
b) Tam giác \(ACD\) nội tiếp trong (O) có \(AD\) là đường kính nên suy ra \(\widehat {ACD} = 90^\circ \)
c) Ta có:
\(AH\) là đường trung trực của \(BC\) (cmt) nên \(H\) là trung điểm cạnh BC.
\(\Rightarrow HB = HC = \dfrac{{BC}}{2}\)\( = \dfrac{{24}}{2} = 12 (cm)\)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACH ta có:
\(A{C^2} = A{H^2} + H{C^2}\)
Suy ra:
\(\eqalign{
& A{H^2} = A{C^2} - H{C^2} \cr
& = {20^2} - {12^2} = 400 - 144 = 256 \cr} \)
\(AH = 16 (cm)\)
Tam giác \(ACD\) vuông tại \(C,\) theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
\(\eqalign{
& A{C^2} = AH.AD \cr
& \Rightarrow AD = {{A{C^2}} \over {AH}} = {{{{20}^2}} \over {16}} = 25 (cm) \cr} \)
Vậy bán kính của đường tròn (O) là :
\(R = \dfrac{{AD}}{2} = \dfrac{{25}}{ 2} = 12,5 (cm)\)
+ Đường tròn là tập hợp các điểm cách điểm O cố định một khoảng bằng R không đổi (\(R>0\)), O gọi là tâm và R là bán kính.
+ Xét tam giác ABC vuông tại A, có đường cao AH:
- Áp dụng định lí Pytago: \(B{C^2} = A{B^2} + A{C^2}\)
- Hệ thức lượng trong tam giác vuông: \(A{C^2} = AH.BC\)
Lời giải chi tiết
a) Tam giác \(ABC\) cân tại \(A\) nên \(AH\) là đường cao đồng thời cũng là đường trung trực của \(BC\).
Vì \(O\) là tâm của đường tròn ngoại tiếp tam giác \(ABC\) nên \(O\) nằm trên đường trung trực của \(BC\) hay \(O\) thuộc \(AD\).
Suy ra \(AD\) là đường kính của (O).
b) Tam giác \(ACD\) nội tiếp trong (O) có \(AD\) là đường kính nên suy ra \(\widehat {ACD} = 90^\circ \)
c) Ta có:
\(AH\) là đường trung trực của \(BC\) (cmt) nên \(H\) là trung điểm cạnh BC.
\(\Rightarrow HB = HC = \dfrac{{BC}}{2}\)\( = \dfrac{{24}}{2} = 12 (cm)\)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACH ta có:
\(A{C^2} = A{H^2} + H{C^2}\)
Suy ra:
\(\eqalign{
& A{H^2} = A{C^2} - H{C^2} \cr
& = {20^2} - {12^2} = 400 - 144 = 256 \cr} \)
\(AH = 16 (cm)\)
Tam giác \(ACD\) vuông tại \(C,\) theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
\(\eqalign{
& A{C^2} = AH.AD \cr
& \Rightarrow AD = {{A{C^2}} \over {AH}} = {{{{20}^2}} \over {16}} = 25 (cm) \cr} \)
Vậy bán kính của đường tròn (O) là :
\(R = \dfrac{{AD}}{2} = \dfrac{{25}}{ 2} = 12,5 (cm)\)