Câu hỏi: Cho hình thoi \( ABCD\) có \(\widehat A = 60^\circ \). Gọi O là giao điểm của hai đường chéo; \( E, F, G, H\) theo thứ tự là trung điểm của \(AB, BC, CD, DA.\) Chứng minh rằng sáu điểm \(E, B, F, G, D, H\) thuộc cùng một đường tròn.
Phương pháp giải
+ Để chứng minh một điểm thuộc một đường tròn cố định thì ta chứng minh điểm đó cách một điểm cố định một khoảng không đổi.
+ Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền.
Lời giải chi tiết
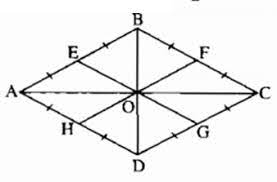
Do \(ABCD\) là hình thoi nên \(AC \bot BD\).
* Xét tam giác vuông \(AOB\) có OE là đường trung tuyến nên:
\(OE = \dfrac{1}{2}AB\)
* Xét tam giác vuông \(COB\) có OF là đường trung tuyến nên:
\(OF = \dfrac{1}{2}BC\)
* Xét tam giác vuông \(COD\) có OG là đường trung tuyến nên:
\(OG = \dfrac{1}{2}DC\)
* Xét tam giác vuông \(AOD\) có OH là đường trung tuyến nên:
\(OH = \dfrac{1}{2}AD\)
Do \(ABCD\) là hình thoi nên \( AB = BC = DC = AD\)
Suy ra \(OE=OF=OG=OH=\dfrac{1}{2}AB\) (1)
* Ta có \(\widehat A = 60^\circ \) (gt) suy ra \(\widehat {OAB} = 30^\circ \) (vì AO là phân giác góc A)
Xét tam giác vuông \(AOB\) ta có: \(OB =AB\sin \widehat {OAB}= \sin 30^\circ .AB\) hay \(OB = \dfrac{1}{2}AB\)
Lại có \(OB=OD\) (vì ABCD là hình thoi)
Nên \(OD =OB = \dfrac{1}{2}AB\) (2)
Từ (1) và (2) suy ra: \(OE=OF=OG=OH=OD=OB\)
Suy ra sáu điểm \(E, B, F, G, D, H\) thuộc cùng một đường tròn tâm \(O\) bán kính \(OB.\)
+ Để chứng minh một điểm thuộc một đường tròn cố định thì ta chứng minh điểm đó cách một điểm cố định một khoảng không đổi.
+ Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền.
Lời giải chi tiết
Do \(ABCD\) là hình thoi nên \(AC \bot BD\).
* Xét tam giác vuông \(AOB\) có OE là đường trung tuyến nên:
\(OE = \dfrac{1}{2}AB\)
* Xét tam giác vuông \(COB\) có OF là đường trung tuyến nên:
\(OF = \dfrac{1}{2}BC\)
* Xét tam giác vuông \(COD\) có OG là đường trung tuyến nên:
\(OG = \dfrac{1}{2}DC\)
* Xét tam giác vuông \(AOD\) có OH là đường trung tuyến nên:
\(OH = \dfrac{1}{2}AD\)
Do \(ABCD\) là hình thoi nên \( AB = BC = DC = AD\)
Suy ra \(OE=OF=OG=OH=\dfrac{1}{2}AB\) (1)
* Ta có \(\widehat A = 60^\circ \) (gt) suy ra \(\widehat {OAB} = 30^\circ \) (vì AO là phân giác góc A)
Xét tam giác vuông \(AOB\) ta có: \(OB =AB\sin \widehat {OAB}= \sin 30^\circ .AB\) hay \(OB = \dfrac{1}{2}AB\)
Lại có \(OB=OD\) (vì ABCD là hình thoi)
Nên \(OD =OB = \dfrac{1}{2}AB\) (2)
Từ (1) và (2) suy ra: \(OE=OF=OG=OH=OD=OB\)
Suy ra sáu điểm \(E, B, F, G, D, H\) thuộc cùng một đường tròn tâm \(O\) bán kính \(OB.\)