Câu hỏi: Tìm các khoảng đồng biến, nghịch biến của các hàm số:
Phương pháp giải:
- Tìm TXĐ.
- Tính \(y'\) theo công thức \(\left( {\dfrac{{ax + b}}{{cx + d}}} \right)' = \dfrac{{ad - bc}}{{{{\left({cx + d} \right)}^2}}}\)
- Xét dấu \(y'\) và kết luận khoảng đồng biến, nghịch biến.
Giải chi tiết:
TXĐ: \(\mathbb{R}\backslash \left\{ { - 7} \right\}\)
\(y' = \dfrac{{ - 2.7 - 3.1}}{{{{\left( {x + 7} \right)}^2}}} = \dfrac{{ - 17}}{{{{\left({x + 7} \right)}^2}}} < 0,\) \(\forall x \ne - 7\)
Vậy hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 7} \right)\) và \(\left( { - 7};+ \infty \right)\).
Phương pháp giải:
- Tìm TXĐ.
- Tính \(y'\) theo công thức \(\left( {\dfrac{1}{u}} \right)' = \dfrac{{ - u'}}{{{u^2}}}\)
- Xét dấu \(y'\) và kết luận khoảng đồng biến, nghịch biến.
Giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ 5 \right\}\)
Ta có: \(y' = \dfrac{{ - \left[ {{{\left( {x - 5} \right)}^2}} \right]'}}{{{{\left({x - 5} \right)}^4}}}\) \(= \dfrac{{ - 2\left( {x - 5} \right)}}{{{{\left({x - 5} \right)}^4}}}\) \(= \dfrac{{ - 2}}{{{{\left( {x - 5} \right)}^3}}}\)
\(y' > 0 \Leftrightarrow \dfrac{{ - 2}}{{{{\left( {x - 5} \right)}^3}}} > 0\) \(\Leftrightarrow {\left( {x - 5} \right)^3} < 0 \Leftrightarrow x < 5\) nên hàm số đồng biến trên khoảng \(\left( { - \infty; 5} \right)\).
\(y' < 0 \Leftrightarrow \dfrac{{ - 2}}{{{{\left( {x - 5} \right)}^3}}} < 0\) \(\Leftrightarrow {\left( {x - 5} \right)^3} > 0 \Leftrightarrow x > 5\) nên hàm số nghịch biến trên khoảng \(\left( {5; + \infty } \right)\).
Phương pháp giải:
- Tìm TXĐ.
- Tính \(y'\) theo công thức \(\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\)
- Xét dấu \(y'\) và kết luận khoảng đồng biến, nghịch biến.
Giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ { \pm 3} \right\}\)
\(y' = \dfrac{{\left( {2x} \right)'.\left({{x^2} - 9} \right) - 2x.\left({{x^2} - 9} \right)'}}{{{{\left({{x^2} - 9} \right)}^2}}}\) \(= \dfrac{{2\left( {{x^2} - 9} \right) - 2x. 2x}}{{{{\left({{x^2} - 9} \right)}^2}}} = \dfrac{{ - 2{x^2} - 18}}{{{{\left({{x^2} - 9} \right)}^2}}}\) \(= \dfrac{{ - 2\left( {{x^2} + 9} \right)}}{{{{\left({{x^2} - 9} \right)}^2}}} < 0,\forall x \in D\)
Vậy hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 3} \right),\left({ - 3; 3} \right),\left({3; + \infty } \right)\).
Phương pháp giải:
- Tìm TXĐ.
- Tính \(y'\) theo công thức \(\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\).
- Xét dấu \(y'\) và kết luận khoảng đồng biến, nghịch biến.
Giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
Ta có: \(y' = \dfrac{{\left( {{x^4} + 48} \right)'. X - \left(x \right)'.\left({{x^4} + 48} \right)}}{{{x^2}}}\) \(= \dfrac{{4{x^3}. X - {x^4} - 48}}{{{x^2}}} = \dfrac{{3{x^4} - 48}}{{{x^2}}}\) \(= \dfrac{{3\left( {{x^4} - 16} \right)}}{{{x^2}}} = \dfrac{{3\left({{x^2} - 4} \right)\left({{x^2} + 4} \right)}}{{{x^2}}}\)
\(y' = 0 \Leftrightarrow {x^2} - 4 = 0 \Leftrightarrow x = \pm 2\).
Bảng biến thiên:
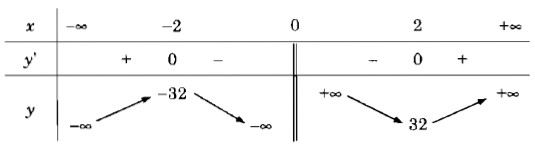
Vậy hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {2; + \infty } \right)\).
Hàm số nghịch biến trên các khoảng \(\left( { - 2; 0} \right)\) và \(\left( {0; 2} \right)\).
Phương pháp giải:
- Tìm TXĐ.
- Tính \(y'\) theo công thức \(\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\).
- Xét dấu \(y'\) và kết luận khoảng đồng biến, nghịch biến.
Giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\)
Ta có: \(y' = \dfrac{{\left( {{x^2} - 2x + 3} \right)'\left({x + 1} \right) - \left({x + 1} \right)'\left({{x^2} - 2x + 3} \right)}}{{{{\left({x + 1} \right)}^2}}}\) \(= \dfrac{{\left( {2x - 2} \right)\left({x + 1} \right) - \left({{x^2} - 2x + 3} \right)}}{{{{\left({x + 1} \right)}^2}}}\) \(= \dfrac{{{x^2} + 2x - 5}}{{{{\left( {x + 1} \right)}^2}}}\)
Khi đó \(y' = 0 \Leftrightarrow {x^2} + 2x - 5 = 0\) \(\Leftrightarrow x = - 1 \pm \sqrt 6 \)
Bảng biến thiên:
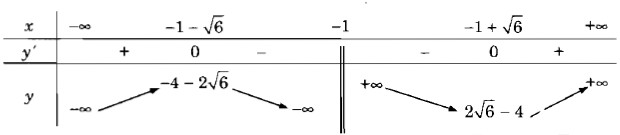
Vậy hàm số đã cho đồng biến trên các khoảng \(( - \infty ; - 1 - \sqrt 6),(- 1 + \sqrt 6 ; + \infty)\)
và nghịch biến trên các khoảng \(( - 1 - \sqrt 6 ; - 1), (- 1; - 1 + \sqrt 6)\)
Phương pháp giải:
- Tìm TXĐ.
- Tính \(y'\) theo công thức \(\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\).
- Xét dấu \(y'\) và kết luận khoảng đồng biến, nghịch biến.
Giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\)
Ta có: \(y' = \dfrac{{\left( {{x^2} - 5x + 3} \right)'\left({x - 2} \right) - \left({x - 2} \right)'\left({{x^2} - 5x + 3} \right)}}{{{{\left({x - 2} \right)}^2}}}\) \(= \dfrac{{\left( {2x - 5} \right)\left({x - 2} \right) - \left({{x^2} - 5x + 3} \right)}}{{{{\left({x - 2} \right)}^2}}}\) \(= \dfrac{{{x^2} - 4x + 7}}{{{{\left( {x - 2} \right)}^2}}}\) \(= \dfrac{{{{\left( {x - 2} \right)}^2} + 3}}{{{{\left({x - 2} \right)}^2}}} > 0,\forall x \in D\).
Vậy hàm số đồng biến trên các khoảng \(\left( { - \infty; 2} \right)\) và \(\left( {2; + \infty } \right)\).
Câu câu a
a) \(y = {{3 - 2x} \over {x + 7}}\)Phương pháp giải:
- Tìm TXĐ.
- Tính \(y'\) theo công thức \(\left( {\dfrac{{ax + b}}{{cx + d}}} \right)' = \dfrac{{ad - bc}}{{{{\left({cx + d} \right)}^2}}}\)
- Xét dấu \(y'\) và kết luận khoảng đồng biến, nghịch biến.
Giải chi tiết:
TXĐ: \(\mathbb{R}\backslash \left\{ { - 7} \right\}\)
\(y' = \dfrac{{ - 2.7 - 3.1}}{{{{\left( {x + 7} \right)}^2}}} = \dfrac{{ - 17}}{{{{\left({x + 7} \right)}^2}}} < 0,\) \(\forall x \ne - 7\)
Vậy hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 7} \right)\) và \(\left( { - 7};+ \infty \right)\).
Câu câu b
b) \(y = {1 \over {{{(x - 5)}^2}}}\)Phương pháp giải:
- Tìm TXĐ.
- Tính \(y'\) theo công thức \(\left( {\dfrac{1}{u}} \right)' = \dfrac{{ - u'}}{{{u^2}}}\)
- Xét dấu \(y'\) và kết luận khoảng đồng biến, nghịch biến.
Giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ 5 \right\}\)
Ta có: \(y' = \dfrac{{ - \left[ {{{\left( {x - 5} \right)}^2}} \right]'}}{{{{\left({x - 5} \right)}^4}}}\) \(= \dfrac{{ - 2\left( {x - 5} \right)}}{{{{\left({x - 5} \right)}^4}}}\) \(= \dfrac{{ - 2}}{{{{\left( {x - 5} \right)}^3}}}\)
\(y' > 0 \Leftrightarrow \dfrac{{ - 2}}{{{{\left( {x - 5} \right)}^3}}} > 0\) \(\Leftrightarrow {\left( {x - 5} \right)^3} < 0 \Leftrightarrow x < 5\) nên hàm số đồng biến trên khoảng \(\left( { - \infty; 5} \right)\).
\(y' < 0 \Leftrightarrow \dfrac{{ - 2}}{{{{\left( {x - 5} \right)}^3}}} < 0\) \(\Leftrightarrow {\left( {x - 5} \right)^3} > 0 \Leftrightarrow x > 5\) nên hàm số nghịch biến trên khoảng \(\left( {5; + \infty } \right)\).
Câu câu c
c) \(y = {{2x} \over {{x^2} - 9}}\)Phương pháp giải:
- Tìm TXĐ.
- Tính \(y'\) theo công thức \(\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\)
- Xét dấu \(y'\) và kết luận khoảng đồng biến, nghịch biến.
Giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ { \pm 3} \right\}\)
\(y' = \dfrac{{\left( {2x} \right)'.\left({{x^2} - 9} \right) - 2x.\left({{x^2} - 9} \right)'}}{{{{\left({{x^2} - 9} \right)}^2}}}\) \(= \dfrac{{2\left( {{x^2} - 9} \right) - 2x. 2x}}{{{{\left({{x^2} - 9} \right)}^2}}} = \dfrac{{ - 2{x^2} - 18}}{{{{\left({{x^2} - 9} \right)}^2}}}\) \(= \dfrac{{ - 2\left( {{x^2} + 9} \right)}}{{{{\left({{x^2} - 9} \right)}^2}}} < 0,\forall x \in D\)
Vậy hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 3} \right),\left({ - 3; 3} \right),\left({3; + \infty } \right)\).
Câu câu d
d) \(y = {{{x^4} + 48} \over x}\)Phương pháp giải:
- Tìm TXĐ.
- Tính \(y'\) theo công thức \(\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\).
- Xét dấu \(y'\) và kết luận khoảng đồng biến, nghịch biến.
Giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
Ta có: \(y' = \dfrac{{\left( {{x^4} + 48} \right)'. X - \left(x \right)'.\left({{x^4} + 48} \right)}}{{{x^2}}}\) \(= \dfrac{{4{x^3}. X - {x^4} - 48}}{{{x^2}}} = \dfrac{{3{x^4} - 48}}{{{x^2}}}\) \(= \dfrac{{3\left( {{x^4} - 16} \right)}}{{{x^2}}} = \dfrac{{3\left({{x^2} - 4} \right)\left({{x^2} + 4} \right)}}{{{x^2}}}\)
\(y' = 0 \Leftrightarrow {x^2} - 4 = 0 \Leftrightarrow x = \pm 2\).
Bảng biến thiên:

Vậy hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {2; + \infty } \right)\).
Hàm số nghịch biến trên các khoảng \(\left( { - 2; 0} \right)\) và \(\left( {0; 2} \right)\).
Câu câu e
e) \(y = {{{x^2} - 2x + 3} \over {x + 1}}\)Phương pháp giải:
- Tìm TXĐ.
- Tính \(y'\) theo công thức \(\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\).
- Xét dấu \(y'\) và kết luận khoảng đồng biến, nghịch biến.
Giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\)
Ta có: \(y' = \dfrac{{\left( {{x^2} - 2x + 3} \right)'\left({x + 1} \right) - \left({x + 1} \right)'\left({{x^2} - 2x + 3} \right)}}{{{{\left({x + 1} \right)}^2}}}\) \(= \dfrac{{\left( {2x - 2} \right)\left({x + 1} \right) - \left({{x^2} - 2x + 3} \right)}}{{{{\left({x + 1} \right)}^2}}}\) \(= \dfrac{{{x^2} + 2x - 5}}{{{{\left( {x + 1} \right)}^2}}}\)
Khi đó \(y' = 0 \Leftrightarrow {x^2} + 2x - 5 = 0\) \(\Leftrightarrow x = - 1 \pm \sqrt 6 \)
Bảng biến thiên:

Vậy hàm số đã cho đồng biến trên các khoảng \(( - \infty ; - 1 - \sqrt 6),(- 1 + \sqrt 6 ; + \infty)\)
và nghịch biến trên các khoảng \(( - 1 - \sqrt 6 ; - 1), (- 1; - 1 + \sqrt 6)\)
Câu câu g
g) \(y = {{{x^2} - 5x + 3} \over {x - 2}}\)Phương pháp giải:
- Tìm TXĐ.
- Tính \(y'\) theo công thức \(\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\).
- Xét dấu \(y'\) và kết luận khoảng đồng biến, nghịch biến.
Giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\)
Ta có: \(y' = \dfrac{{\left( {{x^2} - 5x + 3} \right)'\left({x - 2} \right) - \left({x - 2} \right)'\left({{x^2} - 5x + 3} \right)}}{{{{\left({x - 2} \right)}^2}}}\) \(= \dfrac{{\left( {2x - 5} \right)\left({x - 2} \right) - \left({{x^2} - 5x + 3} \right)}}{{{{\left({x - 2} \right)}^2}}}\) \(= \dfrac{{{x^2} - 4x + 7}}{{{{\left( {x - 2} \right)}^2}}}\) \(= \dfrac{{{{\left( {x - 2} \right)}^2} + 3}}{{{{\left({x - 2} \right)}^2}}} > 0,\forall x \in D\).
Vậy hàm số đồng biến trên các khoảng \(\left( { - \infty; 2} \right)\) và \(\left( {2; + \infty } \right)\).
Rất tiếc, câu hỏi này chưa có lời giải chi tiết. Bạn ơi, đăng nhập và giải chi tiết giúp zix.vn nhé!!!