Câu hỏi: Tìm cực trị của các hàm số sau:
a) \(y = x - 6\root 3 \of {{x^2}} \)
b) \(y = (7 - x)\root 3 \of {x + 5}\)
c) \(y = {x \over {\sqrt {10 - {x^2}} }}\)
d) \(y = {{{x^3}} \over {\sqrt {{x^2} - 6} }}\)
Phương pháp giải:
- Tính \(y'\) và tìm nghiệm.
- Lập bảng biến thiên và kết luận.
Lời giải chi tiết:
TXĐ: R
\(\begin{array}{l}
y = x - 6{x^{\frac{2}{3}}}\\
y' = 1 - 6.\frac{2}{3}{x^{ - \frac{1}{3}}} = 1 - 4.\frac{1}{{{x^{\frac{1}{3}}}}}\\
= 1 - \frac{4}{{\sqrt[3]{x}}} = \frac{{\sqrt[3]{x} - 4}}{{\sqrt[3]{x}}}\\
y' = 0 \Leftrightarrow \sqrt[3]{x} - 4 = 0\\
\Leftrightarrow \sqrt[3]{x} = 4 \Leftrightarrow x = 64
\end{array}\)
Bảng biến thiên:
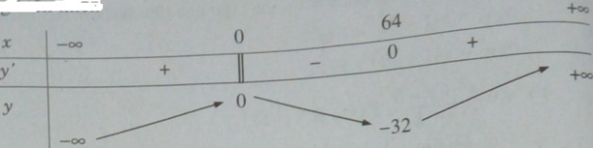
Vậy ta có yCĐ = y(0) = 0 và yCT = y(64) = -32.
Phương pháp giải:
- Tính \(y'\) và tìm nghiệm.
- Lập bảng biến thiên và kết luận.
Lời giải chi tiết:
Hàm số xác định trên \(R\).
\(\begin{array}{l}
y = \left({7 - x} \right){\left({x + 5} \right)^{\frac{1}{3}}}\\
y' = \left({7 - x} \right)'{\left({x + 5} \right)^{\frac{1}{3}}} + \left({7 - x} \right)\left[ {{{\left({x + 5} \right)}^{\frac{1}{3}}}} \right]'\\
= - {\left({x + 5} \right)^{\frac{1}{3}}} + \left({7 - x} \right).\frac{1}{3}{\left({x + 5} \right)^{ - \frac{2}{3}}}
\end{array}\)
\(= - \root 3 \of {x + 5} + {{7 - x} \over {3\root 3 \of {{{(x + 5)}^2}} }} \) \( = \frac{{ - 3\left( {x + 5} \right) + 7 - x}}{{3\sqrt[3]{{{{\left({x + 5} \right)}^2}}}}} = \frac{{ - 4x - 8}}{{3\sqrt[3]{{{{\left({x + 5} \right)}^2}}}}}\)
\(y' = 0 \Leftrightarrow - 4x - 8 = 0 \Leftrightarrow x = - 2\)
Bảng biến thiên:
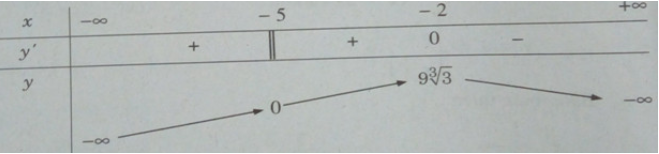
Vậy \({y_{CD}} = y( - 2) = 9\root 3 \of 3 \)
Phương pháp giải:
- Tính \(y'\) và tìm nghiệm.
- Xét dấu \(y'\) và kết luận.
Lời giải chi tiết:
TXĐ: \(D=( - \sqrt {10} ;\sqrt {10})\) .
\(y' = \frac{{\left( x \right)'.\sqrt {10 - {x^2}} - x.\left({\sqrt {10 - {x^2}} } \right)'}}{{\left({\sqrt {10 - {x^2}} } \right)'}}\)
\(= {{\sqrt {10 - {x^2}} + {{{x^2}} \over {\sqrt {10 - {x^2}} }}} \over {10 - {x^2}}} \) \( = \frac{{\frac{{10 - {x^2} + {x^2}}}{{\sqrt {10 - {x^2}} }}}}{{10 - {x^2}}}\) \(= {{10} \over {(10 - {x^2})\sqrt {10 - {x^2}} }}\)
Vì \(y’ > 0\) với mọi \(x\in ( - \sqrt {10} ;\sqrt {10})\) nên hàm số đồng biến trên khoảng đó và do đó không có cực trị.
Phương pháp giải:
- Tính \(y'\) và tìm nghiệm.
- Lập bảng biến thiên và kết luận.
Lời giải chi tiết:
TXĐ: \(D = ( - \infty ; - \sqrt 6) \cup (\sqrt 6 ; + \infty)\)
\(\eqalign{
& y' = \frac{{\left({{x^3}} \right)'\sqrt {{x^2} - 6} + {x^3}\left({\sqrt {{x^2} - 6} } \right)'}}{{{{\left({\sqrt {{x^2} - 6} } \right)}^2}}}\cr &= {{3{x^2}\sqrt {{x^2} - 6} - {{{x^4}} \over {\sqrt {{x^2} - 6} }}} \over {{x^2} - 6}} \cr
& = {{3{x^2}({x^2} - 6) - {x^4}} \over {\sqrt {{{({x^2} - 6)}^3}} }} \cr
& = \frac{{3{x^4} - 18{x^2} - {x^4}}}{{\sqrt {{{\left({{x^2} - 6} \right)}^3}} }} = \frac{{2{x^4} - 18{x^2}}}{{\sqrt {{{\left({{x^2} - 6} \right)}^3}} }}\cr &= {{2{x^2}({x^2} - 9)} \over {\sqrt {{{({x^2} - 6)}^3}} }} \cr} \)
\(y' = 0\)\(\Leftrightarrow 2{x^2}\left( {{x^2} - 9} \right) = 0 \)
\(\Leftrightarrow \left[ \begin{array}{l}
x^2 = 0\\
{x^2} - 9 = 0
\end{array} \right. \) \(\Leftrightarrow \left[ \begin{array}{l}
x = 0 \notin D\\
x = \pm 3 \in D
\end{array} \right.\)
Bảng biến thiên:
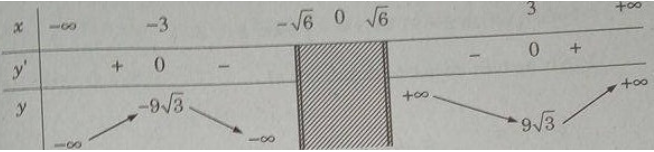
Từ đó ta thấy hàm số đạt cực đại tại \(x = -3\), đạt cực tiểu tại \(x =3\) và \({y_{CT}} = y(3) = 9\sqrt 3 ;\) \({y_{CD}} = y( - 3) = - 9\sqrt 3 \)
a) \(y = x - 6\root 3 \of {{x^2}} \)
b) \(y = (7 - x)\root 3 \of {x + 5}\)
c) \(y = {x \over {\sqrt {10 - {x^2}} }}\)
d) \(y = {{{x^3}} \over {\sqrt {{x^2} - 6} }}\)
Câu a
\(y = x - 6\root 3 \of {{x^2}} \)Phương pháp giải:
- Tính \(y'\) và tìm nghiệm.
- Lập bảng biến thiên và kết luận.
Lời giải chi tiết:
TXĐ: R
\(\begin{array}{l}
y = x - 6{x^{\frac{2}{3}}}\\
y' = 1 - 6.\frac{2}{3}{x^{ - \frac{1}{3}}} = 1 - 4.\frac{1}{{{x^{\frac{1}{3}}}}}\\
= 1 - \frac{4}{{\sqrt[3]{x}}} = \frac{{\sqrt[3]{x} - 4}}{{\sqrt[3]{x}}}\\
y' = 0 \Leftrightarrow \sqrt[3]{x} - 4 = 0\\
\Leftrightarrow \sqrt[3]{x} = 4 \Leftrightarrow x = 64
\end{array}\)
Bảng biến thiên:

Vậy ta có yCĐ = y(0) = 0 và yCT = y(64) = -32.
Câu b
\(y = (7 - x)\root 3 \of {x + 5}\)Phương pháp giải:
- Tính \(y'\) và tìm nghiệm.
- Lập bảng biến thiên và kết luận.
Lời giải chi tiết:
Hàm số xác định trên \(R\).
\(\begin{array}{l}
y = \left({7 - x} \right){\left({x + 5} \right)^{\frac{1}{3}}}\\
y' = \left({7 - x} \right)'{\left({x + 5} \right)^{\frac{1}{3}}} + \left({7 - x} \right)\left[ {{{\left({x + 5} \right)}^{\frac{1}{3}}}} \right]'\\
= - {\left({x + 5} \right)^{\frac{1}{3}}} + \left({7 - x} \right).\frac{1}{3}{\left({x + 5} \right)^{ - \frac{2}{3}}}
\end{array}\)
\(= - \root 3 \of {x + 5} + {{7 - x} \over {3\root 3 \of {{{(x + 5)}^2}} }} \) \( = \frac{{ - 3\left( {x + 5} \right) + 7 - x}}{{3\sqrt[3]{{{{\left({x + 5} \right)}^2}}}}} = \frac{{ - 4x - 8}}{{3\sqrt[3]{{{{\left({x + 5} \right)}^2}}}}}\)
\(y' = 0 \Leftrightarrow - 4x - 8 = 0 \Leftrightarrow x = - 2\)
Bảng biến thiên:

Vậy \({y_{CD}} = y( - 2) = 9\root 3 \of 3 \)
Câu c
\(y = {x \over {\sqrt {10 - {x^2}} }}\)Phương pháp giải:
- Tính \(y'\) và tìm nghiệm.
- Xét dấu \(y'\) và kết luận.
Lời giải chi tiết:
TXĐ: \(D=( - \sqrt {10} ;\sqrt {10})\) .
\(y' = \frac{{\left( x \right)'.\sqrt {10 - {x^2}} - x.\left({\sqrt {10 - {x^2}} } \right)'}}{{\left({\sqrt {10 - {x^2}} } \right)'}}\)
\(= {{\sqrt {10 - {x^2}} + {{{x^2}} \over {\sqrt {10 - {x^2}} }}} \over {10 - {x^2}}} \) \( = \frac{{\frac{{10 - {x^2} + {x^2}}}{{\sqrt {10 - {x^2}} }}}}{{10 - {x^2}}}\) \(= {{10} \over {(10 - {x^2})\sqrt {10 - {x^2}} }}\)
Vì \(y’ > 0\) với mọi \(x\in ( - \sqrt {10} ;\sqrt {10})\) nên hàm số đồng biến trên khoảng đó và do đó không có cực trị.
Câu d
\(y = {{{x^3}} \over {\sqrt {{x^2} - 6} }}\)Phương pháp giải:
- Tính \(y'\) và tìm nghiệm.
- Lập bảng biến thiên và kết luận.
Lời giải chi tiết:
TXĐ: \(D = ( - \infty ; - \sqrt 6) \cup (\sqrt 6 ; + \infty)\)
\(\eqalign{
& y' = \frac{{\left({{x^3}} \right)'\sqrt {{x^2} - 6} + {x^3}\left({\sqrt {{x^2} - 6} } \right)'}}{{{{\left({\sqrt {{x^2} - 6} } \right)}^2}}}\cr &= {{3{x^2}\sqrt {{x^2} - 6} - {{{x^4}} \over {\sqrt {{x^2} - 6} }}} \over {{x^2} - 6}} \cr
& = {{3{x^2}({x^2} - 6) - {x^4}} \over {\sqrt {{{({x^2} - 6)}^3}} }} \cr
& = \frac{{3{x^4} - 18{x^2} - {x^4}}}{{\sqrt {{{\left({{x^2} - 6} \right)}^3}} }} = \frac{{2{x^4} - 18{x^2}}}{{\sqrt {{{\left({{x^2} - 6} \right)}^3}} }}\cr &= {{2{x^2}({x^2} - 9)} \over {\sqrt {{{({x^2} - 6)}^3}} }} \cr} \)
\(y' = 0\)\(\Leftrightarrow 2{x^2}\left( {{x^2} - 9} \right) = 0 \)
\(\Leftrightarrow \left[ \begin{array}{l}
x^2 = 0\\
{x^2} - 9 = 0
\end{array} \right. \) \(\Leftrightarrow \left[ \begin{array}{l}
x = 0 \notin D\\
x = \pm 3 \in D
\end{array} \right.\)
Bảng biến thiên:

Từ đó ta thấy hàm số đạt cực đại tại \(x = -3\), đạt cực tiểu tại \(x =3\) và \({y_{CT}} = y(3) = 9\sqrt 3 ;\) \({y_{CD}} = y( - 3) = - 9\sqrt 3 \)
Rất tiếc, câu hỏi này chưa có lời giải chi tiết. Bạn ơi, đăng nhập và giải chi tiết giúp zix.vn nhé!!!