Xét tất cả các số thực $x, y$ sao cho ${{27}^{5-{{y}^{2}}}}\ge...

Gọi điểm $M\left( x;y \right)$.
Ta có: ${{27}^{5-{{y}^{2}}}}\ge {{a}^{6x-{{\log }_{3}}{{a}^{3}}}}\Leftrightarrow {{3}^{3\left( 5-{{y}^{2}} \right)}}\ge {{a}^{6x-3{{\log }_{3}}a}}\Leftrightarrow 3\left( 5-{{y}^{2}} \right)\ge \left( 6x-3{{\log }_{3}}a \right){{\log }_{3}}a$
$\Leftrightarrow 3{{\log }^{2}}_{3}a-6x{{\log }_{3}}a-3{{y}^{2}}+15\ge 0, \forall a>0$ $\left( 1 \right)$
Đặt $t={{\log }_{3}}a$, ta có $t\in \mathbb{R}, \forall a>0$. Do đó: $\left( 1 \right)\Leftrightarrow 3{{t}^{2}}-6xt-3{{y}^{2}}+15\ge 0, \forall t\in \mathbb{R}$
$\Leftrightarrow {\Delta }'=9{{x}^{2}}+9{{y}^{2}}-45\le 0\Leftrightarrow {{x}^{2}}+{{y}^{2}}-5\le 0 \left( 2 \right)$.
Từ $\left( 2 \right)$ suy ra điểm $M$ thuộc hình tròn $\left( C \right)$ có tâm $O\left( 0;0 \right)$ và bán kính $R=\sqrt{5}$.
Viết lại $P={{x}^{2}}+{{y}^{2}}-4x+8y={{\left( x-2 \right)}^{2}}+{{\left( y+4 \right)}^{2}}-20=A{{M}^{2}}-20$, trong đó $A\left( 2;-4 \right)$.
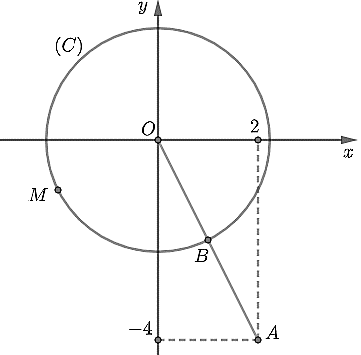Từ hình vẽ, ta có: ${{P}_{\min }}\Leftrightarrow A{{M}_{\min }}\Leftrightarrow M\equiv B\Rightarrow A{{M}_{\min }}=OA-R=\sqrt{5}\Rightarrow {{P}_{\min }}=-15$.