Google
Câu hỏi: Xét khối tứ diện $ABCD$ có cạnh $AD=x$, các cạnh còn lại có cạnh bằng $4\sqrt{3}$. Tìm $x$ để thể tích khối tứ diện $ABCD$ lớn nhất là
A. $2\sqrt{3}$.
B. $6\sqrt{2}$.
C. $3\sqrt{2}$.
D. $2\sqrt{6}$.
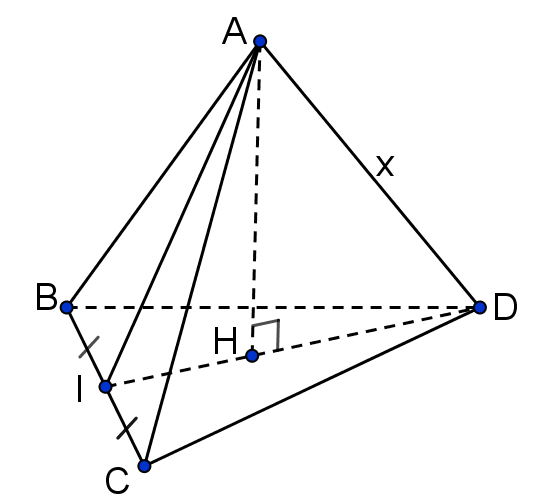Gọi $I$ là trung điểm của $BC$. Từ giả thiết suy ra tam giác $ABC$ và tam giác $DBC$ là các tam giác đều có cạnh bằng $4\sqrt{3}$. Do đó $\left\{ \begin{aligned}
& BC\bot AI \\
& BC\bot DI \\
\end{aligned} \right.\Rightarrow BC\bot \left( AID \right)\Rightarrow \left( AID \right)\bot \left( BCD \right)$.
Trong mặt phẳng $\left( AID \right)$ gọi $H$ là hình chiếu của $A$ lên cạnh $ID$, ta có $AH\bot \left( BCD \right)$.
${{V}_{ABCD}}=\dfrac{1}{3}{{S}_{\Delta BCD}}.AH\le \dfrac{1}{3}{{S}_{\Delta BCD}}.AI=\dfrac{1}{3}{{\left( 4\sqrt{3} \right)}^{2}}.\dfrac{\sqrt{3}}{4}.\left( 4\sqrt{3} \right)\dfrac{\sqrt{3}}{2}=24\sqrt{3}$.
Dấu $''=''$ xảy ra khi $AH=AI\Leftrightarrow H\equiv I\Leftrightarrow x=AI.\sqrt{2}=6\sqrt{2}$. Vậy khi $x=6\sqrt{2}$ thì thể tích tứ diện $ABCD$ lớn nhất.
A. $2\sqrt{3}$.
B. $6\sqrt{2}$.
C. $3\sqrt{2}$.
D. $2\sqrt{6}$.
& BC\bot AI \\
& BC\bot DI \\
\end{aligned} \right.\Rightarrow BC\bot \left( AID \right)\Rightarrow \left( AID \right)\bot \left( BCD \right)$.
Trong mặt phẳng $\left( AID \right)$ gọi $H$ là hình chiếu của $A$ lên cạnh $ID$, ta có $AH\bot \left( BCD \right)$.
${{V}_{ABCD}}=\dfrac{1}{3}{{S}_{\Delta BCD}}.AH\le \dfrac{1}{3}{{S}_{\Delta BCD}}.AI=\dfrac{1}{3}{{\left( 4\sqrt{3} \right)}^{2}}.\dfrac{\sqrt{3}}{4}.\left( 4\sqrt{3} \right)\dfrac{\sqrt{3}}{2}=24\sqrt{3}$.
Dấu $''=''$ xảy ra khi $AH=AI\Leftrightarrow H\equiv I\Leftrightarrow x=AI.\sqrt{2}=6\sqrt{2}$. Vậy khi $x=6\sqrt{2}$ thì thể tích tứ diện $ABCD$ lớn nhất.
Đáp án B.