Google
Câu hỏi: Trong không gian $O x y z$, cho mặt cầu $(S):(x-3)^2+(y-1)^2+z^2=4$ và đường thẳng $d:\left\{\begin{array}{l}x=1+2 t \\ y=-1+t \text {. Gọi }(P) \text { là mặt phẳng chứa } d \text { và cắt }(S) \text { theo một đường tròn có bán kính nhỏ nhất, } \\ z=-t\end{array}\right.$ phương trình của $(P)$ là
A. $3 x-2 y-4 z-8=0$.
B. $x-2 y-3=0$.
C. $y+z+1=0$.
D. $x+3 y+5 z+2=0$.
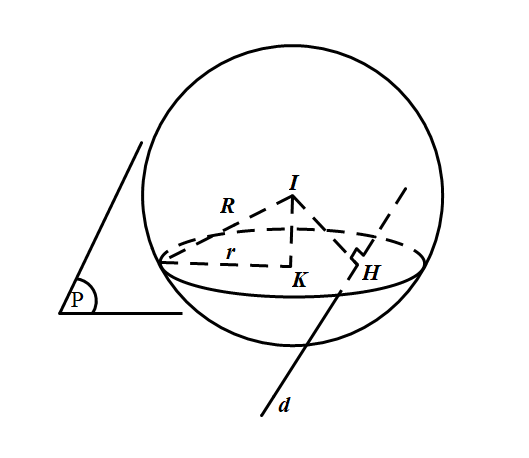Mặt cầu $(S):(x-3)^2+(y-1)^2+z^2=4$ có tâm $I(3 ; 1 ; 0)$ bán kính $R=2$.
Gọi $H$ là hình chiếu vuông góc của $I$ lên $d ; K$ là hình chiếu vuông góc của $I$ lên $(P)$.
Ta có $H \in d$ nên gọi $H(1+2 t ;-1+t ;-t) ; \overrightarrow{I H}=(-2+2 t ;-2+t ;-t)$ ;
Đường thẳng $d$ có vectơ chỉ phương $\vec{u}=(2 ; 1 ;-1)$.
$I H \perp d \Leftrightarrow \overrightarrow{I H} \cdot \vec{u}=\mathbf{0} \Leftrightarrow(-2+2 t) \cdot 2+(-2+t)+(-t) .(-1)=\mathbf{0} \Leftrightarrow \boldsymbol{t}=\mathbf{1} \Rightarrow \boldsymbol{H}(\mathbf{3} ; \mathbf{0} ;-\mathbf{1})$.
Nên $\overrightarrow{I H}=(0 ;-1 ;-1) \Rightarrow I H=\sqrt{2}<R$. Do đó $d$ cắt mặt cầu tại hai điểm. Mặt phẳng $(P)$ cắt mặt cầu $(S)$ theo một đường tròn có bán kính $r=\sqrt{R^2-d^2(I ;(P))}=\sqrt{4-d^2(I ;(P))}$.
Để $r$ nhỏ nhất thì $d(I ;(P))$ lớn nhất.
Ta có $d(I ;(P))=I K \leq I H$.
Do đó $d(I ;(P))$ lớn nhất $\Leftrightarrow I K=I H \Leftrightarrow K \equiv H$.
Khi đó mặt phẳng $(P)$ đi qua $H$ và nhận $\overrightarrow{I H}$ làm vectơ pháp tuyến nên có phương trình là $0 .(x-3)-1 .(y-0)-1 \cdot(z+1)=0$ hay $y+z+1=0$.
Vậy phương trình mặt phẳng $(P): y+z+1=0$.
A. $3 x-2 y-4 z-8=0$.
B. $x-2 y-3=0$.
C. $y+z+1=0$.
D. $x+3 y+5 z+2=0$.
Gọi $H$ là hình chiếu vuông góc của $I$ lên $d ; K$ là hình chiếu vuông góc của $I$ lên $(P)$.
Ta có $H \in d$ nên gọi $H(1+2 t ;-1+t ;-t) ; \overrightarrow{I H}=(-2+2 t ;-2+t ;-t)$ ;
Đường thẳng $d$ có vectơ chỉ phương $\vec{u}=(2 ; 1 ;-1)$.
$I H \perp d \Leftrightarrow \overrightarrow{I H} \cdot \vec{u}=\mathbf{0} \Leftrightarrow(-2+2 t) \cdot 2+(-2+t)+(-t) .(-1)=\mathbf{0} \Leftrightarrow \boldsymbol{t}=\mathbf{1} \Rightarrow \boldsymbol{H}(\mathbf{3} ; \mathbf{0} ;-\mathbf{1})$.
Nên $\overrightarrow{I H}=(0 ;-1 ;-1) \Rightarrow I H=\sqrt{2}<R$. Do đó $d$ cắt mặt cầu tại hai điểm. Mặt phẳng $(P)$ cắt mặt cầu $(S)$ theo một đường tròn có bán kính $r=\sqrt{R^2-d^2(I ;(P))}=\sqrt{4-d^2(I ;(P))}$.
Để $r$ nhỏ nhất thì $d(I ;(P))$ lớn nhất.
Ta có $d(I ;(P))=I K \leq I H$.
Do đó $d(I ;(P))$ lớn nhất $\Leftrightarrow I K=I H \Leftrightarrow K \equiv H$.
Khi đó mặt phẳng $(P)$ đi qua $H$ và nhận $\overrightarrow{I H}$ làm vectơ pháp tuyến nên có phương trình là $0 .(x-3)-1 .(y-0)-1 \cdot(z+1)=0$ hay $y+z+1=0$.
Vậy phương trình mặt phẳng $(P): y+z+1=0$.
Đáp án C.