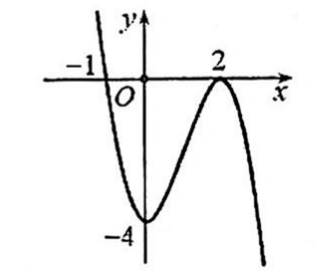
Câu hỏi: Tìm tất cả các giá trị của tham số $m$ để phương trình ${{x}^{3}}-3{{x}^{2}}+4+m=0$ chỉ có một nghiệm duy nhất lớn hơn $2$. Biết rằng đồ thị của hàm số $y=-{{x}^{3}}+3{{x}^{2}}-4$ có hình vẽ như bên dưới.
A. $m\le -4$.
B. $\left[ \begin{aligned}
& m<-4 \\
& m>0 \\
\end{aligned} \right. $.
C. $ m<-4 $.
D. $ m>0$.
A. $m\le -4$.
B. $\left[ \begin{aligned}
& m<-4 \\
& m>0 \\
\end{aligned} \right. $.
C. $ m<-4 $.
D. $ m>0$.
Ta có: ${{x}^{3}}-3{{x}^{2}}+4+m=0\Leftrightarrow -{{x}^{3}}+3{{x}^{2}}-4=m$
Do đó, số nghiệm của phương trình là số giao điểm giữa đồ thị hàm số $\left( C \right)$ : $y=-{{x}^{3}}+3{{x}^{2}}-4$ và đường thẳng $y=m$.
Để phương trình ${{x}^{3}}-3{{x}^{2}}+4+m=0$ có một nghiệm duy nhất lớn hơn $2$ thì đường thẳng $y=m$ cắt đồ thị hàm số $\left( C \right)$ tại một điểm duy nhất có hoành độ lớn hơn 2.
Dựa vào đồ thị ta có $m<-4$.
Do đó, số nghiệm của phương trình là số giao điểm giữa đồ thị hàm số $\left( C \right)$ : $y=-{{x}^{3}}+3{{x}^{2}}-4$ và đường thẳng $y=m$.
Để phương trình ${{x}^{3}}-3{{x}^{2}}+4+m=0$ có một nghiệm duy nhất lớn hơn $2$ thì đường thẳng $y=m$ cắt đồ thị hàm số $\left( C \right)$ tại một điểm duy nhất có hoành độ lớn hơn 2.
Dựa vào đồ thị ta có $m<-4$.
Đáp án C.