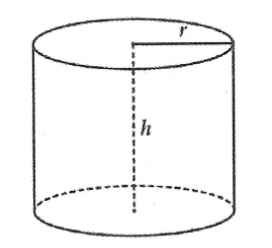
Câu hỏi: Người ta thiết kế một thùng chứa nước hình trụ (như hình vẽ) có thể tích $V$ nhất định. Biết rằng giá của vật liệu làm mặt đáy và nắp thùng bằng nhau và đắt gấp 3 lần so với giá vật liệu để làm mặt xung quanh của thùng (tính trên một đơn vị diện tích). Gọi chiều cao của thùng là $h$ và bán kính đáy là $r$. Tính tỉ số của $\dfrac{h}{r}$ sao cho chi phí sản xuất thùng là nhỏ nhất?
A. $\dfrac{h}{r}=\sqrt{2}$
B. $\dfrac{h}{r}=2$
C. $\dfrac{h}{r}=6$
D. $\dfrac{h}{r}=3\sqrt{2}$

Ta có: $V=\pi {{r}^{2}}h\Leftrightarrow h=\dfrac{V}{\pi {{r}^{2}}}\Rightarrow \dfrac{h}{r}=\dfrac{V}{\pi {{r}^{3}}}$
Gọi $x$ là giá tiền sản xuất một đơn vị diện tích mặt xung quanh.
Chi phí sản xuất mặt xung quanh là:
${{M}_{1}}=x.{{S}_{xq}}=2\pi rhx=2\pi rx\dfrac{V}{\pi {{r}^{2}}}\Rightarrow {{M}_{1}}=\dfrac{2xV}{r}$
Chi phí sản xuất 2 đáy là: ${{M}_{2}}=\left( 3x \right).2{{S}_{day}}=6x.\pi {{r}^{2}}$
Tổng chi phí là: $M={{M}_{1}}+{{M}_{2}}=\dfrac{2xV}{r}+6x.\pi {{r}^{2}}$
$\Rightarrow M=2x\left( \dfrac{V}{r}+3\pi {{r}^{2}} \right)=2x\left( \dfrac{V}{2r}+\dfrac{V}{2r}+3\pi {{r}^{2}} \right)\overset{Cauchy}{\mathop{\ge }} 2x.3\sqrt[3]{\dfrac{V}{2r}.\dfrac{V}{2r}.3\pi {{r}^{2}}}=3x.\sqrt[3]{6\pi {{V}^{2}}}$
$\Rightarrow \min M=3x.\sqrt[3]{6\pi {{V}^{2}}}\Leftrightarrow \dfrac{V}{2r}=3\pi {{r}^{2}}\Leftrightarrow \dfrac{V}{\pi {{r}^{3}}}=6\Rightarrow \dfrac{h}{r}=\dfrac{V}{\pi {{r}^{3}}}=6$

A. $\dfrac{h}{r}=\sqrt{2}$
B. $\dfrac{h}{r}=2$
C. $\dfrac{h}{r}=6$
D. $\dfrac{h}{r}=3\sqrt{2}$
Ta có: $V=\pi {{r}^{2}}h\Leftrightarrow h=\dfrac{V}{\pi {{r}^{2}}}\Rightarrow \dfrac{h}{r}=\dfrac{V}{\pi {{r}^{3}}}$
Gọi $x$ là giá tiền sản xuất một đơn vị diện tích mặt xung quanh.
Chi phí sản xuất mặt xung quanh là:
${{M}_{1}}=x.{{S}_{xq}}=2\pi rhx=2\pi rx\dfrac{V}{\pi {{r}^{2}}}\Rightarrow {{M}_{1}}=\dfrac{2xV}{r}$
Chi phí sản xuất 2 đáy là: ${{M}_{2}}=\left( 3x \right).2{{S}_{day}}=6x.\pi {{r}^{2}}$
Tổng chi phí là: $M={{M}_{1}}+{{M}_{2}}=\dfrac{2xV}{r}+6x.\pi {{r}^{2}}$
$\Rightarrow M=2x\left( \dfrac{V}{r}+3\pi {{r}^{2}} \right)=2x\left( \dfrac{V}{2r}+\dfrac{V}{2r}+3\pi {{r}^{2}} \right)\overset{Cauchy}{\mathop{\ge }} 2x.3\sqrt[3]{\dfrac{V}{2r}.\dfrac{V}{2r}.3\pi {{r}^{2}}}=3x.\sqrt[3]{6\pi {{V}^{2}}}$
$\Rightarrow \min M=3x.\sqrt[3]{6\pi {{V}^{2}}}\Leftrightarrow \dfrac{V}{2r}=3\pi {{r}^{2}}\Leftrightarrow \dfrac{V}{\pi {{r}^{3}}}=6\Rightarrow \dfrac{h}{r}=\dfrac{V}{\pi {{r}^{3}}}=6$
Đáp án C.