Google
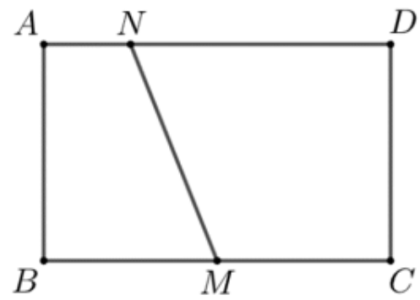
Câu hỏi: Một mảnh bìa hình chữ nhật $ABCD$ có đường chéo $AC=1$. Người ta đánh dấu $M$ là trung điểm của $BC,N$ là điểm thuộc cạnh $AD$ với $AD=4AN$. Sau đó người ta cuốn mảnh bìa lại sao cho cạnh $AB$ trùng với cạnh $CD$ tạo thành một hình trụ (không có hai đáy). Khi đó, các điểm $A, B, M, N$ tạo thành tứ diện $ABMN$.
Tính giá trị lớn nhất của thể tích tứ diện $ABMN$.
A. $\dfrac{\sqrt{3}}{54{{\pi }^{2}}}$.
B. $\dfrac{\sqrt{3}}{18{{\pi }^{2}}}$.
C. $\dfrac{1}{18{{\pi }^{2}}}$.
D. $\dfrac{\sqrt{2}}{18{{\pi }^{2}}}$.
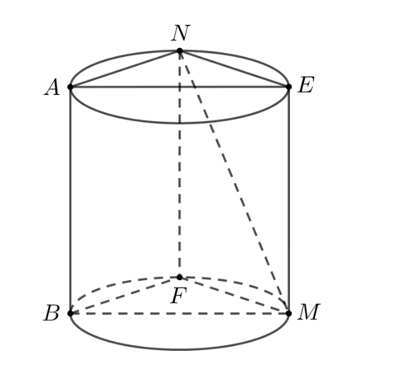sGiả sử hình trụ như hình vẽ. Kẻ các đường sinh $ME$, $NF$. Khi đó $N$ là điểm chính giữa cung $AE$, suy ra tam giác $ANE$ vuông cân tại $N$.
Đặt $BC=a\Rightarrow AB=\sqrt{1-{{a}^{2}}}$. Gọi $R$ là bán kính đường tròn đáy, ta có
Ta có ${{a}^{4}}\left( 1-{{a}^{2}} \right)=\dfrac{1}{2}{{a}^{2}}\cdot {{a}^{2}}\left( 2-2{{a}^{2}} \right)\le \dfrac{1}{2}\cdot {{\left( \dfrac{{{a}^{2}}+{{a}^{2}}+2-2{{a}^{2}}}{3} \right)}^{3}}=\dfrac{4}{27}$.
Dấu “ $=$ ” xảy ra khi và chỉ khi ${{a}^{2}}=2-2{{a}^{2}}\Leftrightarrow {{a}^{2}}=\dfrac{2}{3}\Rightarrow a=\dfrac{\sqrt{6}}{3}$.
Khi đó thể tích tứ diện $ABMN$ là
A. $\dfrac{\sqrt{3}}{54{{\pi }^{2}}}$.
B. $\dfrac{\sqrt{3}}{18{{\pi }^{2}}}$.
C. $\dfrac{1}{18{{\pi }^{2}}}$.
D. $\dfrac{\sqrt{2}}{18{{\pi }^{2}}}$.
Đặt $BC=a\Rightarrow AB=\sqrt{1-{{a}^{2}}}$. Gọi $R$ là bán kính đường tròn đáy, ta có
$AD=2\pi R=a\Rightarrow R=\dfrac{a}{2\pi }\Rightarrow AN=\dfrac{AE}{\sqrt{2}}=\dfrac{2R}{\sqrt{2}}=\dfrac{a}{\sqrt{2}\pi }$.
Ta có ${{V}_{ABMN}}=\dfrac{1}{3}{{V}_{ANE.BMF}}=\dfrac{1}{3}\left( AB\cdot {{S}_{ANE}} \right)=\dfrac{1}{12{{\pi }^{2}}}{{a}^{2}}\sqrt{1-{{a}^{2}}}=\dfrac{1}{12{{\pi }^{2}}}\sqrt{{{a}^{4}}\left( 1-{{a}^{2}} \right)}$.Ta có ${{a}^{4}}\left( 1-{{a}^{2}} \right)=\dfrac{1}{2}{{a}^{2}}\cdot {{a}^{2}}\left( 2-2{{a}^{2}} \right)\le \dfrac{1}{2}\cdot {{\left( \dfrac{{{a}^{2}}+{{a}^{2}}+2-2{{a}^{2}}}{3} \right)}^{3}}=\dfrac{4}{27}$.
Dấu “ $=$ ” xảy ra khi và chỉ khi ${{a}^{2}}=2-2{{a}^{2}}\Leftrightarrow {{a}^{2}}=\dfrac{2}{3}\Rightarrow a=\dfrac{\sqrt{6}}{3}$.
Khi đó thể tích tứ diện $ABMN$ là
${{V}_{ABMN}}=\dfrac{1}{12{{\pi }^{2}}}\cdot \sqrt{\dfrac{4}{27}}=\dfrac{\sqrt{3}}{54{{\pi }^{2}}}$.
Đáp án A.