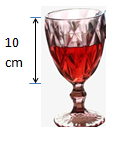
Câu hỏi: Một ly rượu hình Parabol tròn xoay (quay một Parabol quanh trục của nó) có chiều cao là $10 cm$, đường kính miệng ly là $6 cm.$ Biết lượng rượu trong ly có thể tích bằng một nửa thể tích của ly khi đựng đầy rượu. Chiều cao phần rượu có trong ly gần với giá trị nào nhất trong các giá trị dưới đây?
A. $7 cm.$
B. $5 cm.$
C. $6,5 cm.$
D. $5,5 cm.$
A. $7 cm.$
B. $5 cm.$
C. $6,5 cm.$
D. $5,5 cm.$
Chọn hệ trục $Oxy$, với $O\left( 0;0 \right)$ là đáy cốc và tia $Oy$ hướng lên miệng cốc
Do đó, gọi phương trình parabol $\left( P \right)$ là $y=a{{x}^{2}}$ (đi qua gốc $O$ )
Vì $\left( P \right)$ đi qua điểm $A\left( 3;10 \right)\Rightarrow 10=9a\Rightarrow a=\dfrac{10}{9}\to \left( P \right):y=\dfrac{10}{9}{{x}^{2}}$
Suy ra thể tích của ly khi đựng đầy rượu là $V=\pi \int\limits_{-3}^{3}{\dfrac{100{{x}^{4}}}{81}dx}$
Thể tích rượu trong ly là ${{V}_{1}}=\pi \int\limits_{-a}^{a}{\dfrac{100{{x}^{4}}}{81}dx}=\dfrac{1}{2}\times \pi \int\limits_{-3}^{3}{\dfrac{100{{x}^{4}}}{81}dx}\Rightarrow {{a}^{5}}=\dfrac{{{3}^{5}}}{2}\Rightarrow a=\dfrac{3}{\sqrt[5]{2}}$
Vậy chiều cao cần tính là $h=\dfrac{10}{9}.{{\left( \dfrac{3}{\sqrt[5]{2}} \right)}^{2}}\approx 7,578.$
Do đó, gọi phương trình parabol $\left( P \right)$ là $y=a{{x}^{2}}$ (đi qua gốc $O$ )
Vì $\left( P \right)$ đi qua điểm $A\left( 3;10 \right)\Rightarrow 10=9a\Rightarrow a=\dfrac{10}{9}\to \left( P \right):y=\dfrac{10}{9}{{x}^{2}}$
Suy ra thể tích của ly khi đựng đầy rượu là $V=\pi \int\limits_{-3}^{3}{\dfrac{100{{x}^{4}}}{81}dx}$
Thể tích rượu trong ly là ${{V}_{1}}=\pi \int\limits_{-a}^{a}{\dfrac{100{{x}^{4}}}{81}dx}=\dfrac{1}{2}\times \pi \int\limits_{-3}^{3}{\dfrac{100{{x}^{4}}}{81}dx}\Rightarrow {{a}^{5}}=\dfrac{{{3}^{5}}}{2}\Rightarrow a=\dfrac{3}{\sqrt[5]{2}}$
Vậy chiều cao cần tính là $h=\dfrac{10}{9}.{{\left( \dfrac{3}{\sqrt[5]{2}} \right)}^{2}}\approx 7,578.$
Đáp án A.