Google
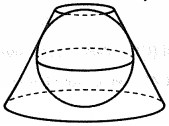
Câu hỏi: Một khối cầu nằm trong một khối nón cụt sao cho mặt cầu tiếp xúc với tất cả các đường sinh và hai hình tròn đáy của khối nón cụt đó. Biết rằng thể tích của khối nón cụt bằng hai lần thể tích của khối cầu. Tỉ số bán kính hình tròn đáy lớn và bán kính hình tròn đáy nhỏ của khối nón cụt bằng
A. $\dfrac{1+\sqrt{5}}{2}$
B. $\sqrt{3}$
C. $\dfrac{3+\sqrt{5}}{2}$
D. $\dfrac{3}{2}$
B. $\sqrt{3}$
C. $\dfrac{3+\sqrt{5}}{2}$
D. $\dfrac{3}{2}$
Giả sử bán kính đáy nhỏ của hình nón cụt bằng 1 và bán kính đáy lớn của hình nón cụt bằng r, với $r>1$. Gọi s là bán kính của mặt cầu thì độ dài trục của hình nón cụt là $h=2s$.
Cắt hình nón cụt và mặt cầu bằng mặt phẳng chứa trục của hình nón cụt ta có hình phẳng như bên.
Dựa vào hình vẽ, ta có ${{\left( 2s \right)}^{2}}+{{\left( r-1 \right)}^{2}}={{\left( r+1 \right)}^{2}}\Leftrightarrow r={{s}^{2}}$.
Thể tích khối cầu là ${{V}_{1}}=\dfrac{4}{3}\pi {{s}^{3}}$, thể tích khối nón cụt là ${{V}_{2}}=\dfrac{1}{3}\pi h\left( {{r}^{2}}+r+1 \right)=\dfrac{2}{3}\pi s\left( {{r}^{2}}+r+1 \right)$
Theo giả thiết ${{V}_{2}}=2{{V}_{1}}$ nên ta có $\dfrac{2}{3}\pi s\left( {{r}^{2}}+r+1 \right)=2.\dfrac{4}{3}\pi {{s}^{3}}\Leftrightarrow {{r}^{2}}+r+1=4{{s}^{2}}$
Suy ra ${{r}^{2}}+r+1=4r\Leftrightarrow {{r}^{2}}-3r+1=0\Leftrightarrow r=\dfrac{3+\sqrt{5}}{2}$ (do $r>1$ )
Vậy tỉ số giữa bán kính hình tròn đáy lớn và bán kính hình tròn đáy nhỏ của khối nón cụt bằng $\dfrac{3+\sqrt{5}}{2}$
Cắt hình nón cụt và mặt cầu bằng mặt phẳng chứa trục của hình nón cụt ta có hình phẳng như bên.
Thể tích khối cầu là ${{V}_{1}}=\dfrac{4}{3}\pi {{s}^{3}}$, thể tích khối nón cụt là ${{V}_{2}}=\dfrac{1}{3}\pi h\left( {{r}^{2}}+r+1 \right)=\dfrac{2}{3}\pi s\left( {{r}^{2}}+r+1 \right)$
Theo giả thiết ${{V}_{2}}=2{{V}_{1}}$ nên ta có $\dfrac{2}{3}\pi s\left( {{r}^{2}}+r+1 \right)=2.\dfrac{4}{3}\pi {{s}^{3}}\Leftrightarrow {{r}^{2}}+r+1=4{{s}^{2}}$
Suy ra ${{r}^{2}}+r+1=4r\Leftrightarrow {{r}^{2}}-3r+1=0\Leftrightarrow r=\dfrac{3+\sqrt{5}}{2}$ (do $r>1$ )
Vậy tỉ số giữa bán kính hình tròn đáy lớn và bán kính hình tròn đáy nhỏ của khối nón cụt bằng $\dfrac{3+\sqrt{5}}{2}$
Đáp án C.