Gọi $S$ là tập hợp các số phức $z=a+bi\left( a,b\in \mathbb{R}...

Đầu tiên ta có $z=a+bi(a,b\in \mathbb{R})$ thì khi đó $|z+\bar{z}|+|z-\bar{z}|=4\iff \left|a\right|+\left|b\right|=2,ab>0.$
Do ${\displaystyle \frac{z_1-z_2}{1+i}}$ là số thực dương nên khi $M\left(z_1\right),N\left(z_2\right)$ thì ta có:
$\overrightarrow{OM}-\overrightarrow{ON}=\overrightarrow{NM}=k(1+i)=k\overrightarrow{OE}(k\in {\mathbb{R}}^{+})$ với $E(1;1).$
Do $ab>0$ nên tập hợp các điểm $M,N$ thuộc $S$ biểu diễn như hình vẽ sau:
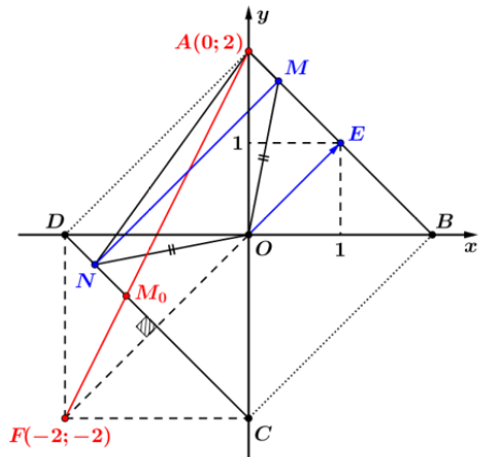Gọi $F(-2;-2)$ là điểm đối xứng với $O$ qua đoạn thẳng $CD$
Suy ra $P=\left|z_1\right|+|z_2-2i|=MO+NA=NO+NA=NF+NA\ge FA=2\sqrt{5}$
Dấu bằng xảy ra khi và chỉ khi $M\equiv M_0=AF\cap CD.$ Chọn đáp án $C$.